Convolutional Layer 역전파(backpropagation)
Convoluational Layer Backpropagation
Numpy로 Deeplearing code를 구현하면서 공부한 내용입니다.
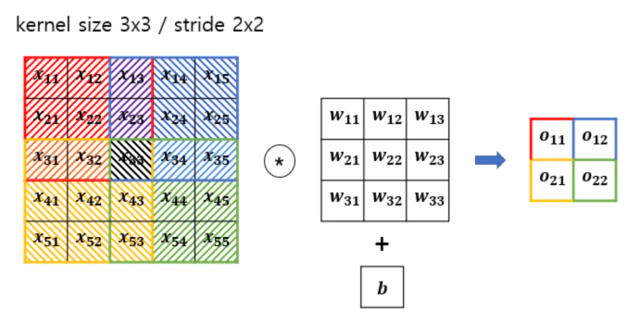
위와 같은 예시에서 수식을 정리해보면
\[O = W * X + b = \begin{pmatrix} o_{11} & o_{12} \\ o_{21} & o_{22} \end{pmatrix}\\ \begin{split} o_{11} &= x_{11} w_{11} + x_{12} w_{12} + x_{13} w_{13} \\ &\quad\; x_{21} w_{21} + x_{22} w_{22} + x_{23} w_{23} \\ &\quad\; x_{31} w_{31} + x_{32} w_{32} + x_{33} w_{33} + b\\ \\ o_{12} &= x_{13} w_{11} + x_{14} w_{12} + x_{15} w_{13} \\ &\quad\; x_{23} w_{21} + x_{24} w_{22} + x_{25} w_{23} \\ &\quad\; x_{33} w_{31} + x_{34} w_{32} + x_{35} w_{33} + b\\ \\ o_{21} &= x_{31} w_{11} + x_{32} w_{12} + x_{33} w_{13} \\ &\quad\; x_{41} w_{21} + x_{42} w_{22} + x_{43} w_{23} \\ &\quad\; x_{51} w_{31} + x_{52} w_{32} + x_{53} w_{33} + b\\ \\ o_{22} &= x_{33} w_{11} + x_{34} w_{12} + x_{35} w_{13} \\ &\quad\; x_{43} w_{21} + x_{44} w_{22} + x_{45} w_{23} \\ &\quad\; x_{53} w_{31} + x_{54} w_{32} + x_{55} w_{33} + b\\ \end{split}\]backward시 다음과 같은 gradient값이 앞선 Layer로부터 들어오게 된다.
\[\frac{\partial L}{\partial O} = \begin{pmatrix} \frac{\partial L}{\partial o_{11}} & \frac{\partial L}{\partial o_{12}} \\ \frac{\partial L}{\partial o_{21}} & \frac{\partial L}{\partial o_{22}} \end{pmatrix}\]backpropagation을 진행하기 위해서 다음 Layer로 전달해줘야할 gradient $\frac{\partial L}{\partial X}$와 weight, bias를 update하기 위한 $\frac{\partial L}{\partial W}$, $\frac{\partial L}{\partial b}$을 계산해야한다.
Input X에 대한 gradient $\frac{\partial L}{\partial X}$ 계산
먼저 $\frac{\partial L}{\partial X}$의 $x_{ij}$에 대한 gradient matrix는 다음과 같이 표현된다.
\[\frac{\partial L}{\partial X} = \begin{pmatrix} \frac{\partial L}{\partial x_{11}} & \frac{\partial L}{\partial x_{12}} & \frac{\partial L}{\partial x_{13}} & \frac{\partial L}{\partial x_{14}} & \frac{\partial L}{\partial x_{15}} \\ \frac{\partial L}{\partial x_{21}} & \frac{\partial L}{\partial x_{22}} & \frac{\partial L}{\partial x_{23}} & \frac{\partial L}{\partial x_{24}} & \frac{\partial L}{\partial x_{25}} \\ \frac{\partial L}{\partial x_{31}} & \frac{\partial L}{\partial x_{32}} & \frac{\partial L}{\partial x_{33}} & \frac{\partial L}{\partial x_{34}} & \frac{\partial L}{\partial x_{35}} \\ \frac{\partial L}{\partial x_{41}} & \frac{\partial L}{\partial x_{42}} & \frac{\partial L}{\partial x_{43}} & \frac{\partial L}{\partial x_{44}} & \frac{\partial L}{\partial x_{45}} \\ \frac{\partial L}{\partial x_{51}} & \frac{\partial L}{\partial x_{52}} & \frac{\partial L}{\partial x_{53}} & \frac{\partial L}{\partial x_{54}} & \frac{\partial L}{\partial x_{55}} \\ \end{pmatrix}\]$x_{11}$에 대해서만 계산해보면 다음과 같이 gradient의 합으로 구성되어있다.
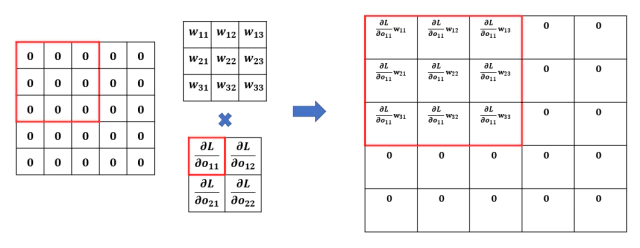
\[\begin{split} \frac{\partial L}{\partial x_{11}} &= \frac{\partial L}{\partial O} \frac{\partial O}{\partial x_{11}} \\ &= \sum^{(2,2)}_{i,j=(1,1)}{ \frac{\partial L}{\partial o_{ij}} \frac{\partial o_{ij}}{\partial x_{11}} } \\ &= \frac{\partial L}{\partial o_{11}} \frac{\partial o_{11}}{\partial x_{11}} + \frac{\partial L}{\partial o_{12}} \frac{\partial o_{12}}{\partial x_{11}} + \frac{\partial L}{\partial o_{21}} \frac{\partial o_{21}}{\partial x_{11}} + \frac{\partial L}{\partial o_{22}} \frac{\partial o_{22}}{\partial x_{11}} \\ &= \frac{\partial L}{\partial o_{11}} \cdot w_{11} + \frac{\partial L}{\partial o_{12}} \cdot 0 + \frac{\partial L}{\partial o_{21}} \cdot 0 + \frac{\partial L}{\partial o_{22}} \cdot 0 \\ \end{split}\]다음 순서의 x에 대해서도 조금더 계산해보면
\[\begin{split} \frac{\partial L}{\partial x_{12}} &= \frac{\partial L}{\partial o_{11}} \cdot w_{12} \\ \frac{\partial L}{\partial x_{13}} &= \frac{\partial L}{\partial o_{11}} \cdot w_{13} + \frac{\partial L}{\partial o_{12}} \cdot w_{11} \\ \frac{\partial L}{\partial x_{14}} &= \frac{\partial L}{\partial o_{12}} \cdot w_{12} \\ \frac{\partial L}{\partial x_{15}} &= \frac{\partial L}{\partial o_{12}} \cdot w_{13} \\ ... \end{split}\]계산되는 값들을 보면 forward 과정에서 convoluation했던 순서와 동일하게 같은 stride로 backporopagation에서도 weight와 gradient값으로 convolution 연산을 하고 있다.
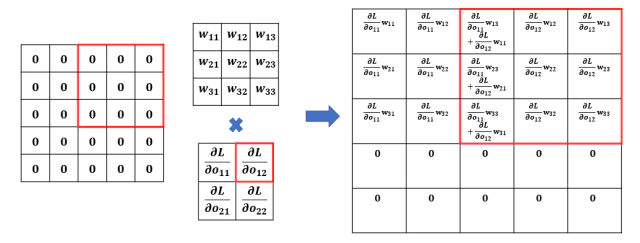
Weight에 대한 gradient $\frac{\partial L}{\partial W}$ 계산
$\frac{\partial L}{\partial W}$를 matrix로 표현하면 다음과 같다.
\[\frac{\partial L}{\partial W} = \begin{pmatrix} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\ \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}} \\ \frac{\partial L}{\partial w_{31}} & \frac{\partial L}{\partial w_{32}} & \frac{\partial L}{\partial w_{33}} \\ \end{pmatrix}\]원소 $w_{11}$에 대한 gradient는 다음과 같이 계산된다.
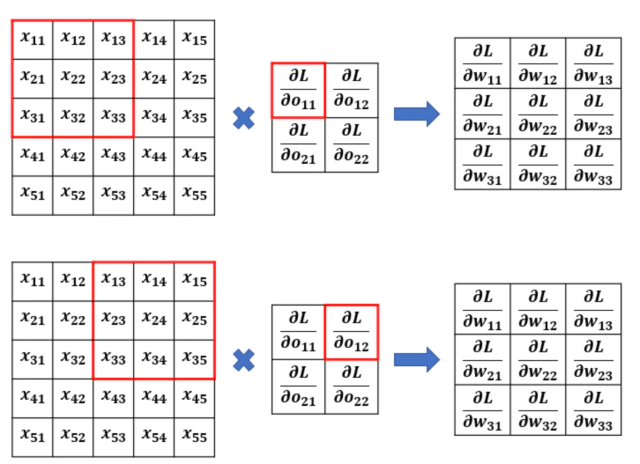
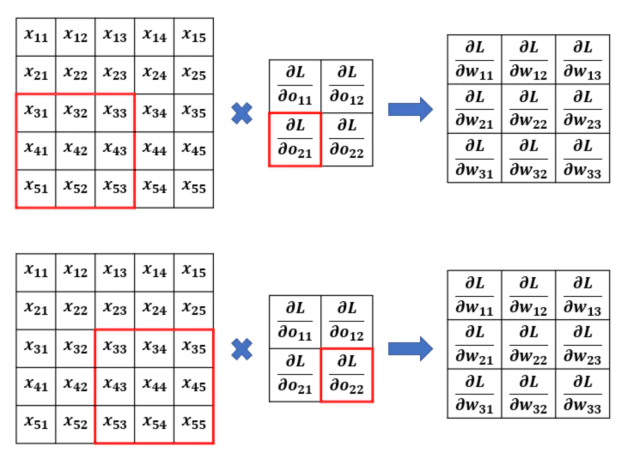
\[\begin{split} \frac{\partial L}{\partial w_{11}} &= \frac{\partial L}{\partial O} \frac{\partial O}{\partial w_{11}} \\ &= \sum^{(2,2)}_{i,j=(1,1)}{\frac{\partial L}{\partial o_{ij}} \frac{\partial o_{ij}}{\partial w_{11}}} \\ &= \frac{\partial L}{\partial o_{11}} \frac{\partial o_{11}}{\partial w_{11}} + \frac{\partial L}{\partial o_{12}} \frac{\partial o_{12}}{\partial w_{11}} + \frac{\partial L}{\partial o_{21}} \frac{\partial o_{21}}{\partial w_{11}} + \frac{\partial L}{\partial o_{22}} \frac{\partial o_{22}}{\partial w_{11}} \\ &= \frac{\partial L}{\partial o_{11}} \cdot x_{11} + \frac{\partial L}{\partial o_{12}} \cdot x_{13} + \frac{\partial L}{\partial o_{21}} \cdot x_{31} + \frac{\partial L}{\partial o_{22}} \cdot x_{33} \\ \end{split}\]계산된 gradient는 $w_{11}$와 forward convolution 과정에서 한번이라도 연관된 값과 앞선 Layer의 gradient값을 곱한 값의 합과 같다.
X에 대한 gradient를 계산할 때와 마찬가지로 forward의 동일한 순서와 stride를 가지는 convolution으로 weight gradient값이 계산된다.
Bias b에 대한 gradient $\frac{\partial L}{\partial b}$ 계산
위에서 계산했던 W, X에 비해 bias의 gradient는 간단하게 다음과 같이 계산된다.
\[\begin{split} \frac{\partial L}{\partial b} &= \frac{\partial L}{\partial O} \frac{\partial O}{\partial b} \\ &= \sum^{(2,2)}_{i,j=(1,1)}{ \frac{\partial L}{\partial o_{ij}} \frac{\partial o_{ij}}{\partial b} } \\ &= \frac{\partial L}{\partial o_{11}} \frac{\partial o_{11}}{\partial b} + \frac{\partial L}{\partial o_{12}} \frac{\partial o_{12}}{\partial b} + \frac{\partial L}{\partial o_{21}} \frac{\partial o_{21}}{\partial b} + \frac{\partial L}{\partial o_{22}} \frac{\partial o_{22}}{\partial b} \\ &= \frac{\partial L}{\partial o_{11}} \cdot 1 + \frac{\partial L}{\partial o_{12}} \cdot 1 + \frac{\partial L}{\partial o_{21}} \cdot 1 + \frac{\partial L}{\partial o_{22}} \cdot 1 \\ &= \sum^{(2,2)}_{i,j=(1,1)}{ \frac{\partial L}{\partial o_{ij}} } \end{split}\]모든 bias에 대한 $\frac{\partial o_{ij}}{\partial b}$이 1로 계산되므로 결국 들어온 gradient를 합한 값이 된다.

Leave a comment