DeepLearning cupy, Numpy로 구현해보기

---

Github 링크

https://github.com/kimjiil/DeepLearningWithNumpy

---

Objectives

Pytorch code

• 전체적인 구조는 코드 문법등은 Pytorch와 유사하게 하려고함.

pytorch code 펼치기/접기

device = torch.device("cuda:0" if torch.cuda.is_available() else 'cpu')

my_train_dataset = Dataset(root='./')
my_valid_dataset = Dataset(root='./')
my_train_datalaoder = DataLoader(Dataset=my_train_dataset, transform=transform, shuffle=True, batch_size=10)
my_valid_dataloader = DataLoader(Dataset=my_valid_dataset, transform=transform, shuffle=False, batch_size=10)

class myModel(nn.Module):
    def __init__(self):
        super(myModel, self).__init__()
    
        self.layer1 = nn.Sequential(
            nn.Linear(in_feature=10, out_feature=20),
            nn.ReLU(),
            nn.BatchNorm2d()
        )
        self.layer2 = nn.Sequential(
            nn.Conv2d(64, 128, kernel_size=3, strides=1, padding=1),
            nn.ReLU(),
            nn.BatchNorm2d()
        )
    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        return x

model = myModel()

if pretrained:
    model.load_statd_dict(pretrained)

optimizer = AdamW(model.parameters(), lr=0.001)
criterion = MSE()

model.to(device)
criterion.to(device)

for i in range(epoch):
    model.train()
    for _batch in my_train_datalaoder:
        optimizer.zero_grad()
        output = model(_batch)
        loss = criterion(output, label)
        loss.backward()
        optimizer.step()

    model.eval()
    for _batch in my_valid_dataloader:
        output = model(_batch)

Numba, cupy, Numpy Matrix Multiplication Calc Time

• numpy에서 그치지않고 GPU에 data를 올려 연산하는 과정까지 구현
  • GPU knernel을 사용하는 언어로 Numba, cupy, cuda-python 3가지중 하나를 선택
• Numba(GPU, CPU), Numpy의 속도가 비슷하고 cupy가 빨라서 cupy 사용
• Why are cuda gpu matrix multiplies slower than numpy? How is numpy so fast?

nvprof으로 측정한 Numba code tack time 결과 펼치기

• Numpy, Numba에서 같은 크기의 matrix multiplication calc time

==5688== NVPROF is profiling process 5688, command: python numba_test.py
<Managed Device 0>
Numpy CPU - 1.1220035552978516s

------------------------------------------------------------------------------------------------------
==5688== Profiling application: python numba_test.py
==5688== Profiling result:
   Start  Duration            Grid Size      Block Size     Regs*    SSMem*    DSMem*      Size  Throughput  SrcMemType  DstMemType           Device   Context    Stream  Name
325.82ms  21.908ms                    -               -         -         -         -  97.656MB  4.3532GB/s    Pageable      Device  NVIDIA GeForce          1         7  [CUDA memcpy HtoD]
347.94ms  397.56ms                    -               -         -         -         -  97.656MB  245.64MB/s    Pageable      Device  NVIDIA GeForce          1         7  [CUDA memcpy HtoD]
746.28ms  4.18387s          (500 500 1)       (16 16 1)        41  2.0000KB        0B         -           -           -           -  NVIDIA GeForce          1         7  cudapy::__main__::fast_matmul$241(Array<double, int=2, C, mutable, aligned>, Array<double, int=2, C, mutable, aligned>, Array<double, int=2, C, mutable, aligned>) [151]
4.93015s  4.11571s          (500 500 1)       (16 16 1)        41  2.0000KB        0B         -           -           -           -  NVIDIA GeForce          1         7  cudapy::__main__::fast_matmul$241(Array<double, int=2, C, mutable, aligned>, Array<double, int=2, C, mutable, aligned>, Array<double, int=2, C, mutable, aligned>) [154]
9.04586s  126.57ms                    -               -         -         -         -  488.28MB  3.7673GB/s      Device    Pageable  NVIDIA GeForce          1         7  [CUDA memcpy DtoH]

Regs: Number of registers used per CUDA thread. This number includes registers used internally by the CUDA driver and/or tools and can be more than what the compiler shows.
SSMem: Static shared memory allocated per CUDA block.
DSMem: Dynamic shared memory allocated per CUDA block.
SrcMemType: The type of source memory accessed by memory operation/copy
DstMemType: The type of destination memory accessed by memory operation/copy

Numpy, Numba, cupy tack time 결과 펼치기

from numba import cuda, float32
import cupy
import numpy as np
import math
import time

TPB = 16
@cuda.jit
def fast_matmul(A, B, C):
    """
    Perform matrix multiplication of C = A * B
    Each thread computes one element of the result matrix C
    """

    # Define an array in the shared memory
    # The size and type of the arrays must be known at compile time
    sA = cuda.shared.array(shape=(TPB, TPB), dtype=float32)
    sB = cuda.shared.array(shape=(TPB, TPB), dtype=float32)

    x, y = cuda.grid(2)

    tx = cuda.threadIdx.x
    ty = cuda.threadIdx.y

    if x >= C.shape[0] and y >= C.shape[1]:
        # Quit if (x, y) is outside of valid C boundary
        return

    # Each thread computes one element in the result matrix.
    # The dot product is chunked into dot products of TPB-long vectors.
    tmp = 0.
    for i in range(int(A.shape[1] / TPB)):
        # Preload data into shared memory
        sA[tx, ty] = A[x, ty + i * TPB]
        sB[tx, ty] = B[tx + i * TPB, y]

        # Wait until all threads finish preloading
        cuda.syncthreads()

        # Computes partial product on the shared memory
        for j in range(TPB):
            tmp += sA[tx, j] * sB[j, ty]

        # Wait until all threads finish computing
        cuda.syncthreads()

    C[x, y] = tmp

N = 1024
a = np.random.randn(N, N).astype(np.float32)
b = a.T.copy()
c = np.zeros((N, N), dtype=np.float32)

threadsperblock = (16, 16)
blockspergrid_x = math.ceil(a.shape[0] / threadsperblock[0])
blockspergrid_y = math.ceil(a.shape[1] / threadsperblock[1])
blockspergrid = (blockspergrid_x, blockspergrid_y)

a_d = cuda.to_device(a)
b_d = cuda.to_device(b)
c_d = cuda.to_device(c)

gfcalc = lambda t0, t1: round(t1-t0, 5)

for i in range(0, 10):
  t0 = time.time()
  fast_matmul[blockspergrid, threadsperblock](a, b, c)
  cuda.synchronize()
  t1 = time.time()
  print("Numba CPU calc Time", gfcalc(t0, t1))

Numba CPU calc Time 0.54381
Numba CPU calc Time 0.062
Numba CPU calc Time 0.061
Numba CPU calc Time 0.04901
Numba CPU calc Time 0.04642
Numba CPU calc Time 0.04843
Numba CPU calc Time 0.046
Numba CPU calc Time 0.04922
Numba CPU calc Time 0.04578
Numba CPU calc Time 0.048

for i in range(0, 10):
  t0 = time.time()
  fast_matmul[blockspergrid, threadsperblock](a_d, b_d, c_d)
  cuda.synchronize()
  t1 = time.time()
  print("Numba GPU calc Time", gfcalc(t0, t1))

Numba GPU calc Time 0.06
Numba GPU calc Time 0.056
Numba GPU calc Time 0.05
Numba GPU calc Time 0.041
Numba GPU calc Time 0.04104
Numba GPU calc Time 0.04101
Numba GPU calc Time 0.03995
Numba GPU calc Time 0.041
Numba GPU calc Time 0.041
Numba GPU calc Time 0.041

for i in range(0, 10):
  t0 = time.time()
  c_h = a.dot(b)
  t1 = time.time()
  print("Numpy calc Time", gfcalc(t0, t1))

Numpy calc Time 0.05517
Numpy calc Time 0.008
Numpy calc Time 0.01207
Numpy calc Time 0.01093
Numpy calc Time 0.01001
Numpy calc Time 0.011
Numpy calc Time 0.01099
Numpy calc Time 0.01003
Numpy calc Time 0.01097
Numpy calc Time 0.01107

with cupy.cuda.Device(0) as dev:
  a_c = cupy.asarray(a)
  b_c = cupy.asarray(b)
  c_c = cupy.asarray(c)
  for i in range(0, 10):
    t0 = time.time()
    a_c.dot(b_c, out=c_c)
    dev.synchronize()
    t1 = time.time()
    print("cupy GPU calc Time", gfcalc(t0, t1))

cupy GPU calc Time 1.02841
cupy GPU calc Time 0.002
cupy GPU calc Time 0.00209
cupy GPU calc Time 0.00091
cupy GPU calc Time 0.002
cupy GPU calc Time 0.001
cupy GPU calc Time 0.002
cupy GPU calc Time 0.001
cupy GPU calc Time 0.002
cupy GPU calc Time 0.001

구현 상세

myLib

• 내부 모듈이 아닌 외부 모듈에서 Tensor 관련 연산을 할때 내부 모듈의 연산 함수를 부르기 위한 Wrapper 함수

• Wrapper를 통해 현재 call한 함수의 이름으로 내부 모듈에서 getattr으로 method를 가져와 연산함

• 첫번째 인자가 myTensor일 경우 해당 Tensor의 내부 모듈을 사용함 ```python from .Module import * import sys module_op = op()

def _Warpper(name, args, **kwargs): if isinstance(args[0], myTensor): return getattr(args[0].op, name)(args, *kwargs) else: return getattr(module_op, name)(args, **kwargs)

def argmax(*args, **kwargs): cur_func_name = sys._getframe().f_code.co_name return _Warpper(cur_func_name, *args, **kwargs) …

#### operator process

- pytorch처럼 Tensor로 감싸고 연산자로는 내부의 data만 계산하는 과정을 따라하고 싶어서 myTensor라는 class를 만들고
python 연산자에 의해 call되는 magic method를 재정의 해주고 연산자에 따라 binary인지 unary인지 나누었음.

```python
    def __add__(self, other):
        return self.binary_operator_function_call(operator.add, other=other)
    ...
    def __neg__(self):
        return self.unary_operator_function_call(operator.neg)

• 연산자가 magic method를 call하면 해당 operator를 wrapper 함수의 파라미터로 주고 해당 operator를 통해 .data에 저장된 값을 연산하고 결과값을 새로운 myTensor를 만들어 할당해줌

    def binary_operator_function_call(self, operator, other):
        if isinstance(other, myTensor):
            temp_data = other.data
            if other.backward_prev:
                temp_prev = other.backward_prev
        else:
            temp_data = other
        if self.backward_prev:
            temp_prev = self.backward_prev

        _new_data = operator(self.data, temp_data)
        _new = myTensor(_new_data)
        _new.grad_fn = f"{operator}"
        _new.op = self.op
        _new.backward_fn = temp_prev
        _new.backward_prev = temp_prev
        return _new

backward process

• pytorch에서 마지막 loss 함수에서 나온 값에 .backward()를 해주면 자동적으로 forward의 역순으로 backward가 실행되는 과정을 구현하고 싶었음.

• 이 과정을 구현하고 싶어 myTensor에 이전 Module의 backward 함수를 저장할 수 있도록 .backward_prev attribute를 사용함

• Module의 forward_call 함수에서 다음과같이 Tensor가 지나갈 때 마다 이전 backward 함수를 갱신하도록 함

    def forward_call(self, *args, **kwargs):
        if args[0].backward_prev:
            self.backward_fn = args[0].backward_prev
        else:
            self.backward_fn = args[0].backward_fn
        args[0].backward_prev = self.backward

        return self.forward(*args, **kwargs)

    __call__: Callable[..., Any] = forward_call

• 모든 Layer나 sequence , tensor는 모두 최상위 myModule class를 상속받기 때문에 모든 과정에서 기록됨.

myModule class

• pytorch는 모델을 Module로 생성하고 sub module과 현재 module이 갖고있는 parameter를 저장한다.
• class myModule을 만들어 _modules에 sub module을 저장하고 _paramters에 parameter들을 저장한다.
• Model()에서 function call이 일어나면 하위 module들의 forward 함수가 호출되도록 함
• pytorch와 마찬가지로 .to()를 호출할 경우 모든 parameter 및 module이 설정한 device에서 돌도록 함
  • 단순히 numpy 와 cupy를 스위칭하는 형식으로 구현함.
• parameters 함수를 호출하면 하위 모듈에 있는 모든 weight들이 포함된 Iterator가 리턴됨.
  • 이를 위해 childretn 함수를 호츌하여 하위 모듈이 모두 call되도록하고 각각 모듈에서 self._parameters에 param이 있을 경우 이를 yield하도록함
  • child에서 yield되어 생성된 Iterator를 다시 상위에서 yield시켜 하위 모듈에서 불린 parameter들이 자동으로 merge 되도록 함.

    def parameters(self):
        # return trainable parameters iterator
        for child in self.children():
            params = child.parameters() #여기서 generator 리턴받음
            for p in params:
                yield p

        for param in self._parameters:
            yield self._parameters[param]

mySequential class

• mySequential class는 다음과 같이 Layer들을 argument로 받고 class를 function call할 경우 자동으로 Layer들을 순서대로 forward해준다.

Layer_seq = mySequential(
                Linear(in_features=20, out_features=10, bias=True),
                ReLU(),
            )

• myModule class를 상속받고 argument로 들어오는 Layer들을 추가하는 코드만 __init__ 부분에 추가 했음.

class mySequential(myModule):
    def __init__(self, *args):
        super(mySequential, self).__init__()

        for idx, module in enumerate(args):
            self.add_module(str(idx), module)

• 외부에서 mySequential의 forward함수를 class하면 class가 갖고 있는 _modules에 있는 모듈들을 불러와 순서대로 forward 함수를 call한다.

    def forward(self, x):
        module = self.__dict__['_modules']
        for module_key in module:
            x = module[module_key].forward(x)
        return x

• 마찬가지로 외부에서 backward 함수를 call할 경우 forward와는 반대로 모듈의 역순으로 backward 함수를 call한다.

    def backward(self, *args, **kwargs):
        back = args[0]
        module = self.__dict__['_modules']
        for module_key in reversed(module):
            back = module[module_key].backward(back)

        self.backward_fn(back)

• 여기서 self.backward_fn은 다음 순서의 모듈의 backward 함수의 주소를 갖고 있고 function call할 경우 그 다음 순서의 모듈 backward 함수가 call된다.

myParameter class

• 이 클래스는 Layer의 weight나 bias를 저장할때 사용한다. 현재 별다른 기능은 구현되있지않고 단순히 myTensor를 상속받아 사용한다.

class myParameter(myTensor):
    def __init__(self, data):
        super(myParameter, self).__init__(data)

myTensor class

• pytorch에서 backward와 각종 연산을 처리하기 위해서 Tensor라는 변수를 사용한다. 여기서도 backward 및 각종 연산을 처리하기 위해 myTensor라는 class를 만들어 처리하기로 함.
• cupy, Numpy 둘다 ndarray를 사용하여 계산이 가능하기 때문에 myTensor에 ndarray를 저장하여 이를 사용해서 계산하기로 함
• .grad와 .grad_fn을 attribute로 갖고 backward시 사용함. (연산자 단위로 backward를 하도록 구현하는건 시간이 너무 오래걸려서 보류)
• myTensor와 myModule에 self.backward_fn에 이전 모듈의 backward 함수를 저장함.
• Numpy와 cupy의 객체를 따로 저장하는 변수를 만들고 하위 함수를 call하는 wrapper 함수를 만듬
  • 예를 들어 cupyTensor로 만들어진 변수들을 더하기 할 경우 wrapper 함수 내부에서 numpy.add 함수를 다시 call 하는 형식

a = myTensor(np.array([1, 2]))
b = myTensor(np.array([3, 4]))

c = a + b # np.ndarray([4,6])

• 위 코드에서 a + b를 실행할 경우 myTensor class의 __add__ 함수가 call되고 __add__ 함수는 더하기 연산이 이항 연산자이므로 self.binary_operator_funtion_call 함수를 operator.add와 other=b를 argument로 call한다.
• self.binary_operator_funtion_call 함수는 myTensor.data에 저장된 ndarray를 argument로 받은 연산자로 계산하고 이 값을 가지고 새로운 myTensor를 생성하여 연산의 결과로 반환 해준다.

class myTensor(myModule):
    ...
    def binary_operator_function_call(self, operator, other):
        if isinstance(other, myTensor):
            temp_data = other.data
        else:
            temp_data = other

        _new_data = operator(self.data, temp_data)
        _new = myTensor(_new_data)
        _new.grad_fn = f"{operator}"
        _new.op = self.op
        _new.backward_fn = self.backward_prev
        _new.backward_prev = self.backward_prev
        return _new
    ...
    def __add__(self, other):
        return self.binary_operator_function_call(operator.add, other=other)
    ...

• myTensor를 cpu가 아닌 gpu에서 사용할 경우 다음과 같이 .to(),.to(device="cuda:0") 함수를 call한다. 함수 인자로 아무것도 주지 않는 경우 자동으로 gpu id 0번에 할당됨.

a_cuda = myTensor(np.array([1,2])).to()

• .to() 함수가 호출될 경우 class 내부에서 cupy의 setDeivce 함수를 호출하고 numpy array에서 cupy array로 변경해준다.
• myTensor끼리의 연산에서 사용될 library도 numpy에서 cupy로 변경해준다.
• 반대로 .to("cpu")가 호출될 경우 cupy에서 numpy로 변경하고 data를 numpy array로 변경하고 gpu에 할당되었던 array의 메모리를 해제한다.

    import cupy as cp
    import numpy as np
    
    class myTensor(myModule):
    ...
    def to(self, *args, **kwargs):
        ...
        if "cuda" in _args:
            cp.cuda.runtime.setDevice(int(_args.split(":")[-1]))
            self.op.set_op(cp)
            self.data = cp.asarray(self.data)
        elif "cpu" in _args:
            self.op.set_op(np)
            self.data = cp.asnumpy(self.data)
            cp._default_memory_pool.free_all_blocks()
    ...

• myTensor는 module을 통과하면서 통과한 이전 module의 backward 함수를 .backward_prev 속성에 저장한다.
• module내에서 연산자를 통해 새로 생성된 myTensor의 경우 연산에 참여한 myTensor의 .backward_prev를 가져간다. 이 과정에서 중간에서 생성된 myTensor들이 어떤 module에서 생성되었는지 기록해서 backward시에 사용함.

class myTensor(myModule):
    ...
    def binary_operator_function_call(self, operator, other):
        if isinstance(other, myTensor):
            temp_data = other.data
        else:
            temp_data = other
    
        _new_data = operator(self.data, temp_data)
        _new = myTensor(_new_data)
        _new.grad_fn = f"{operator}"
        _new.op = self.op
        _new.backward_fn = self.backward_prev
        _new.backward_prev = self.backward_prev
        return _new

Layer

---

Conv2d

구현 상세 펼치기/접기

Conv2d의 구현에 관한 증명은 여기서설명한다.

$(N,C,H_{in},W_{in})$ 이미지에서 $(kH,kW)$의 크기를 가지는 kernel window을 움직이면서 convolution 연산을 진행해서 output $(N,C,H_{out},W_{out})$를 생성함.

\[out(N_i, C_{out_j}) = bias(C_{out_j}) + \sum^{C_{in} - 1}_{k=0}{weight(C_{out_j}, k) * input(N_i, k) }\]

• Parameters
  • kernel_size (Union[int, Tuple[int, int]]) - max 값을 추출한 window의 크기
  • stride (Union[int, Tuple[int, int]]) - window를 이동시킬 거리
  • padding (Union[int, Tuple[int, int]]) - zero padding의 크기
  • dilation (Union[int, Tuple[int, int]]) - window를 이동시킬 거리를 조절하는 파라미터(감소)
  • bias (bool, optional) - True이면 bias를 추가함. Default: True
• Input : $(N,C,H_{in},W_{in})$
• Output : $(N,C,H_{out},W_{out})$

\[H_{out} = \bigg{\lfloor} \frac{H_{in} + 2 * padding[0] - dilation[0] \times (kernel_size[0] - 1) - 1}{stride[0]} + 1\bigg{\rfloor} \\ W_{out} = \bigg{\lfloor} \frac{W_{in} + 2 * padding[1] - dilation[1] \times (kernel_size[1] - 1) - 1}{stride[1]} + 1\bigg{\rfloor}\]

init하는 부분에서 parameter로 int단일로 들어오면 self._set_tuple함수로 tuple로 변경해준다.

구현된 코드는 다음과 같다.

class Conv2d(BaseLayer):
    def __init__(self,
                 in_channels,
                 out_channels,
                 kernel_size,
                 stride=1,
                 padding=0,
                 dilation=1,
                 bias=True):
        super(Conv2d, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = self._set_tuple(kernel_size)
        self.stride = self._set_tuple(stride)
        self.padding = self._set_tuple(padding)
        self.dilation = self._set_tuple(dilation)

        _k = np.sqrt(1 / (self.in_channels * self.kernel_size[0] * self.kernel_size[1]))

        if bias:
            #create bias
            self.bias = myParameter(self.op.random.uniform(low=-_k, high=_k, size=self.out_channels))
        else:
            self.bias = None

        self.weight = myParameter(self.op.random.uniform(low=-_k, high=_k,
                                                         size=(self.in_channels,
                                                               self.kernel_size[0],
                                                               self.kernel_size[1],
                                                               self.out_channels)))

    def forward(self, x: myTensor) -> myTensor:
        self._backward_save = x
        N, C, self.H_in, self.W_in = x.shape

        self.H_out = int((self.H_in + 2 * self.padding[0] - self.dilation[0] * (self.kernel_size[0] - 1) - 1) / self.stride[0] + 1)
        self.W_out = int((self.W_in + 2 * self.padding[1] - self.dilation[1] * (self.kernel_size[1] - 1) - 1) / self.stride[1] + 1)

        self.H_padding = self.H_in + 2 * self.padding[0]
        self.W_padding = self.W_in + 2 * self.padding[1]

        padding_x = self.op.zeros((N, C, self.H_in + 2 * self.padding[0], self.W_in + 2 * self.padding[1]))
        padding_x[:, :, self.padding[0]:self.H_padding - self.padding[0], self.padding[1]:self.W_padding - self.padding[1]] = x

        output = self.op.zeros((N, self.out_channels, self.H_out, self.W_out))

        for h in range(self.H_out):
            h_start = h * self.stride[0]
            h_end = h * self.stride[0] + self.kernel_size[0]
            for w in range(self.W_out):
                w_start = w * self.stride[1]
                w_end = w * self.stride[1] + self.kernel_size[1]
                window = padding_x[:, :, h_start:h_end, w_start:w_end] 
                window = self.op.reshape(window, (N, self.in_channels, self.kernel_size[0], self.kernel_size[1], 1))
               
                _out = window * self.op.reshape(self.weight, (1, self.in_channels, self.kernel_size[0], self.kernel_size[1], self.out_channels))
                if self.bias:
                    _out = self.op.sum(_out, axis=(1, 2, 3)) + self.bias
                else:
                    _out = self.op.sum(_out, axis=(1, 2, 3))

                output[:, :, h, w] = _out

        return output

    def _backward(self, *args, **kwargs):
        _back_in = args[0]

        N, C, self.H_in, self.W_in = self._backward_save.shape

        self.weight.grad = self.op.zeros_like(self.weight)
        if self.bias:
            self.bias.grad = self.op.zeros_like(self.bias)

        padding_x = self.op.zeros((N, C, self.H_in + 2 * self.padding[0], self.W_in + 2 * self.padding[1]))
        _back_gradient = self.op.zeros_like(padding_x)

        padding_x[:, :, self.padding[0]:self.H_padding - self.padding[0], self.padding[1]:self.W_padding - self.padding[1]] = self._backward_save

        for h_i in range(self.H_out):
            h_start = h_i * self.stride[0]
            h_end = h_start + self.kernel_size[0]
            for w_i in range(self.W_out):
                w_start = w_i * self.stride[1]
                w_end = w_start + self.kernel_size[1]

                # calculate weight gradient
                window_x = padding_x[:, :, h_start:h_end, w_start:w_end].reshape((N, self.in_channels, self.kernel_size[0], self.kernel_size[1], 1))
                _grad = self.op.transpose(_back_in[:, :, h_i, w_i].reshape((N, self.out_channels, 1, 1, 1)), axes=(0, 4, 2, 3, 1))
                self.weight.grad += self.op.sum(window_x * _grad, axis=0)

                if self.bias:
                    self.bias.grad += self.op.sum(_back_in[:, :, h_i, w_i], axis=0)

                window_backgradient = _grad * self.weight.reshape((1, *self.weight.shape))
                _back_gradient[:, :, h_start:h_end, w_start:w_end] += self.op.sum(window_backgradient, axis=-1)

        return _back_gradient[:, :, self.padding[0]:self.H_padding - self.padding[0], self.padding[1]:self.W_padding - self.padding[1]]

---

Linear

구현 상세 펼치기/접기

init 함수에서 in out의 dim을 결정하고 그에 따른 weight와 bias를 생성한다. 이때 weight의 랜덤한 범위는 xavier 공식에 따른다.

class Linear(BaseLayer):
    def __init__(self, in_features: int, out_features: int, bias: bool = True):
        super(Linear, self).__init__()

        self.in_features = in_features
        self.out_features = out_features

        _k = np.sqrt(1/in_features)
        self.weight = myParameter(self.op.random.uniform(low=-_k, high=_k, size=(in_features, out_features)))
        if bias:
            self.bias = myParameter(self.op.random.uniform(low=-_k, high=_k, size=out_features))

forward함수에서는 bias가 True일때와 False일때를 나누어서 계산하도록 하고 backward함수를 위해 input을 저장한다.

    def forward(self, x: myTensor): # N C_in -> N C_out
        self._backward_save = x
        if self.bias:
            x = self.op.matmul(x, self.weight) + self.bias
        else:
            x = self.op.matmul(x, self.weight)
        return x

Linear Layer Backpropagation에 관한 증명은 다음 링크에서 설명한다.

[Linear Layer Back propagation 증명]

\[\frac{\partial Loss}{\partial W} = X^{T} \frac{\partial Loss}{\partial Y} \\ \frac{\partial Loss}{\partial X} = \frac{\partial Loss}{\partial Y} W^{T} \\ \frac{\partial Loss}{\partial B} = C^{T} \frac{\partial Loss}{\partial Y}\]

$C^{T}$는 broadcast matrix로 Sum함수로 대체 가능하다.

    def _backward(self, *args, **kwargs):
        self._update_w = self.op.matmul(self.op.transpose(self._backward_save), args[0])
        self._update_b = self.op.sum(args[0], axis=0)
        _back = self.op.matmul(args[0], self.op.transpose(self.weight))
        return _back

---

BatchNorm2d

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

ReLU

구현 상세 펼치기/접기

[pytorch Document - ReLU]

\[ReLU(x) = (x)^{+} = max(0, x)\]

• forward 함수는 max함수를 사용해서 간단하게 구현.

    def forward(self, x: myTensor):
        self._backward_save = x > 0
        return self.op.maximum(0, x)

• backward할때 ReLU함수는 forward에서 0보다 큰 신호에 대해서만 back gradient를 전달한다. 0보다 작아 나가지 않은 back gradient는 뒤로 전달하지 않음(Loss를 계산하는데 전혀 영향을 주지 않았기 때문에)

• forward할때 미리 back gradient mask인 self._backward_save를 계산해서 저장해놓음

    def _backward(self, *args, **kwargs):
       return self._backward_save * args[0]

---

MaxPool2d

구현 상세 펼치기/접기

$(N,C,H,W)$ 이미지에서 $(kH,kW)$의 크기를 가지는 kernel window을 움직이면서 window 내에서 최대값 1개를 뽑아 output으로 함

• Input : $(N,C,H_{in},W_{in})$

• Output : $(N,C,H_{out},W_{out})$

• Parameters
  • kernel_size (Union[int, Tuple[int, int]]) - max 값을 추출한 window의 크기
  • stride (Union[int, Tuple[int, int]]) - window를 이동시킬 거리
  • padding (Union[int, Tuple[int, int]]) - zero padding의 크기
  • dilation (Union[int, Tuple[int, int]]) - window를 이동시킬 거리를 조절하는 파라미터(감소)

\[H_{out} = \bigg{\lfloor} \frac{H_{in} + 2 * padding[0] - dilation[0] \times (kernel_size[0] - 1) - 1}{stride[0]} + 1\bigg{\rfloor} \\ W_{out} = \bigg{\lfloor} \frac{W_{in} + 2 * padding[1] - dilation[1] \times (kernel_size[1] - 1) - 1}{stride[1]} + 1\bigg{\rfloor}\]

init하는 부분에서 parameter로 int단일로 들어오면 self._set_tuple함수로 tuple로 변경해준다.

class MaxPool2d(BaseLayer):
    def __init__(self, kernel_size, stride=None, padding=0, dilation=1):
        super(MaxPool2d, self).__init__()
        self.kernel_size = self._set_tuple(kernel_size)
        self.padding = self._set_tuple(padding)
        self.stride = self._set_tuple(stride)
        self.dilation = self._set_tuple(dilation)

    def _set_tuple(self, param):
        if isinstance(param, tuple):
            return param
        elif isinstance(param, int):
            return tuple([param, param])
        else:
            raise TypeError

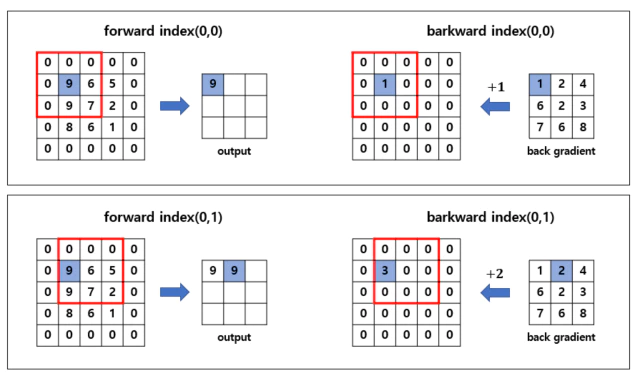
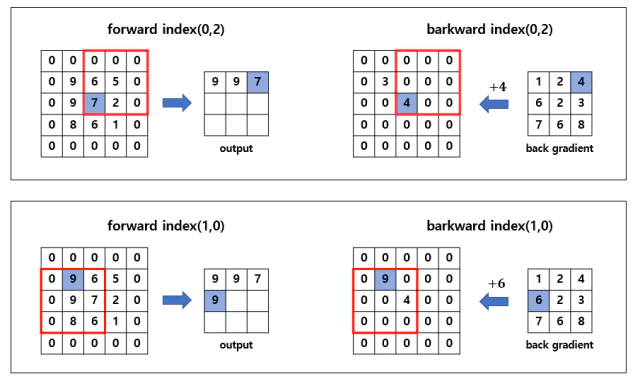
forward에서는 먼저 Input x에 zero padding을 씌워주고 kernel_size만큼 slice한 window에서 max값을 뽑아 output으로 뽑고 해당 index를 backward를 위해 self._back_coord에 저장한다.

small_mask는 window에서 같은 값이 있을 경우 2개의 값이 뽑히는걸 방지하기 위해 서로 다른 epsilon값을 더해줘서 중복되는 값을 제거함.

    def forward(self, x: myTensor) -> myTensor:
        # N C H_in W_in -> N C H_out W_out
        # C H_in W_in -> C H_out W_out
        x_shape = x.shape
        N, C, self.H_in, self.W_in = x_shape[:]

        padding_x = self.op.zeros(x_shape[:-2] + tuple([self.H_in + 2 * self.padding[0], self.W_in + 2 * self.padding[1]]))

        self._back_coord = dict()

        padding_x[:, :, self.padding[0]:(self.H_in+self.padding[0]), self.padding[1]:(self.W_in+self.padding[1])] = x

        H_out = int((self.H_in + 2 * self.padding[0] - self.dilation[0] * (self.kernel_size[0] - 1) - 1) / self.stride[0] + 1)
        W_out = int((self.W_in + 2 * self.padding[1] - self.dilation[1] * (self.kernel_size[1] - 1) - 1) / self.stride[1] + 1)

        new_shape = x_shape[:-2] + tuple([H_out, W_out])
        out_matrix = self.op.zeros(new_shape)

        ##########################################################################
        small_mask = self.op.reshape(self.op.arange(self.kernel_size[0] * self.kernel_size[1], 0, -1), (self.kernel_size[0], self.kernel_size[1]))* np.finfo(float).eps * 10
        small_mask = self.op.tile(small_mask, [N, C, 1, 1])
        ##########################################################################

        for h in range(H_out):
            h_start = self.stride[0] * h
            h_end = self.stride[0] * h + self.kernel_size[0]
            for w in range(W_out):
                w_start = self.stride[1] * w
                w_end = self.stride[1] * w + self.kernel_size[1]

                kernel = padding_x[:, :, h_start:h_end, w_start:w_end] + small_mask
                max_value = self.op.max(kernel, axis=(-2, -1))
                out_matrix[:, :, h, w] = max_value
                self._back_coord[(h, w)] = kernel >= max_value.reshape((N, C, 1, 1))

        return out_matrix

backward는 아까 저장된 self._back_coord를 사용해서 output으로 출력된 index만 back gradient를 전달한다.

    def _backward(self, *args, **kwargs):
        N, C, H_out, W_out = args[0].shape
        _back_gradient = self.op.zeros(tuple([N, C] + [self.H_in + 2 * self.padding[0], self.W_in + 2 * self.padding[1]]))
        for h in range(H_out):
            h_start = self.stride[0] * h
            h_end = self.stride[0] * h + self.kernel_size[0]
            for w in range(W_out):
                w_start = self.stride[1] * w
                w_end = self.stride[1] * w + self.kernel_size[1]

                _back_mask = self._back_coord[(h, w)] * args[0][:, :, h:h+1, w:w+1]
                _back_gradient[:, :, h_start:h_end, w_start:w_end] += _back_mask

        return _back_gradient[:, :, self.padding[0]:self.H_in + 1 - self.padding[0], self.padding[1]:self.W_in + 1 - self.padding[1]]

---

AvgPool

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

Flatten

구현 상세 펼치기/접기

forward는 다음과 같은 shape를 가진 tensor가 들어오면 start, end사이의 shape를 곱한 값으로 합쳐주면 된다.

• Input : $(*,S_{start}, … , S_{i}, … , S_{end}, *)$ 여기서 $S_{i}$는 $i$차원의 size를 뜻하고, *는 차원의 개수과 상관없이 어떤 사이즈가 와도 상관없음을 뜻함.
• Output : $(*, \prod^{end}_{i=start} S_{i}, *)$

backward함수에서는 back gradient으로 들어오는 값을 원래 Input x의 shape로 변경해주면 된다.

class Flatten(BaseLayer): 
    def __init__(self, start_dim=1, end_dim=-1):
        super(Flatten, self).__init__()
        self.start_dim = start_dim
        self.end_dim = end_dim

    def forward(self, x: myTensor) -> myTensor:
        x_shape = x.shape
        self._original_shape = x.shape

        _shape = np.prod(x_shape[self.start_dim:self.end_dim])
        new_shape = x_shape[:self.start_dim] + tuple([_shape]) + x_shape[self.end_dim:]

        out = self.op.reshape(x, new_shape)

        return out

    def _backward(self, *args, **kwargs):
        back = self.op.reshape(args[0], self._original_shape)
        return back

---

Sigmoid

구현 상세 펼치기/접기

forward값은 다음과 같이 계산된다.

\[Sigmoid(x) = \sigma (x) = \frac{1}{1 + exp(-x)}\]

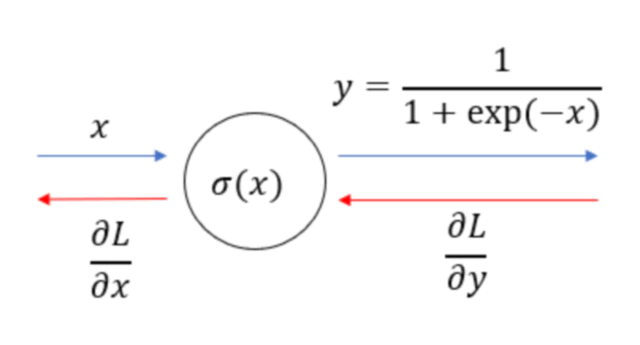
upstream gradient로 $\frac{\partial L}{\partial y}$가 들어오고 downstream gradient $\frac{\partial L}{\partial x}$를 계산해야 된다. 이를 chain rule로 나타내면 다음과 같다.

\[\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial x}\] \[\begin{split} y &= \frac{1}{1 + exp(-x)} = \frac{1}{t} \;\; , \, t = 1+exp(-x)\\ \frac{\partial y}{\partial x} &= -\frac{1}{t^{2}} \frac{\partial t}{\partial x} = \frac{1}{t^{2}} exp(-x) = \frac{exp(-x)}{(1 + exp(-x))^{2}} \\ &= (1-y)y \end{split}\]

$(1-y)y$을 downstream gradient로 보내주면 되므로 forward에서 $y$를 저장하고 이를 backward에서 upstream과 합쳐서 내려보내준다.

    def forward(self, x: myTensor):
        self._backward_save = 1 / (1 + self.op.exp(-x))
        return self._backward_save

    def _backward(self, *args, **kwargs):
        return args[0] * self._backward_save * (1 - self._backward_save)

---

Dropout

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

Opimizer

---

Adam

구현 상세 펼치기/접기

momentum과 RMSProp를 혼합한 optimizer로 다음과 같이 update를 진행한다.

\[m_{t} = \beta_{1} \cdot m_{t-1} + (1 - \beta_{1}) \cdot g_{t} \\ v_{t} = \beta_{2} \cdot v_{t-1} + (1 - \beta_{2}) \cdot g_{t}^{2} \\ \hat{m}_{t} = \frac{m_{t}}{1 - \beta_{1}^{t}} \\ \hat{v}_{t} = \frac{v_{t}}{1 - \beta_{2}^{t}} \\ \theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_{t} + \epsilon}} \cdot \hat{m}_{t}\]

$m_{0}=0, v_{0}=0$은 $0$으로 초기화 되고 $\beta_{1}=0.9, \; \beta_{2}=0.999$의 값을 default로 한다.

class Adam(BaseOptimizer):
    def __init__(self, parameters, beta1=0.9, beta2=0.999, lr=0.001, eps=1e-8):
        super(Adam, self).__init__(parameters, lr)
        self.beta1 = beta1
        self.beta2 = beta2
        self.eps = eps

    def step(self):
        for param in self.params_list:
            op = param._get_op()
            if not '_m' in param._opt_file and not '_v' in param._opt_file:
                param._opt_file['_m'] = op.zeros_like(param.grad)
                param._opt_file['_v'] = op.zeros_like(param.grad)

            param._opt_file['_m'] = self.beta1 * param._opt_file['_m'] + (1 - self.beta1) * param.grad
            param._opt_file['_v'] = self.beta2 * param._opt_file['_v'] + (1 - self.beta2) * (param.grad ** 2)

            biased_mt = param._opt_file['_m'] / (1 - self.beta1 ** self.step_t)
            biased_vt = param._opt_file['_v'] / (1 - self.beta2 ** self.step_t)
            test = self.learning_rate / (op.sqrt(biased_vt) + self.eps)
            _update = param - test  * biased_mt
            param.update_parameter(_update)
        self.step_t += 1

---

AdamW

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

Stochastic Gradient Descent

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

Loss function

---

Mean Square Error

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

Cross Entropy

구현 상세 펼치기/접기

Test Code 입니다.
Test Code 입니다.
Test Code 입니다.

---

구현할때 사용한 Tip

Python

• 어떤 class를 만들때 __new__ 을 먼저 call해서 메모리를 할당한 이후 __init__을 call한다.
• instance를 생성한 class를 function call하게 되면 class의 __call__ 함수를 호출한다. __call__함수를 정의할 경우 class의 instance 를 callable하게 바꿔준다.
• 어떤 class의 instance에서 Temp[:,0]을 하면 class의 __getitem__ 함수를 call한다.
• 어떤 class의 instance에서 Temp[3] = 3와 같은 리스트 할당을 하게 되면 class의 __setitem__ 함수를 call한다.
• 어떤 class의 instance에서 Temp1 + Temp2와 같은 operator call이 일어나면 해당 operator에 대한 함수를 call한다. 여기서는 +이므로 __add__를 call한다.

[operator call에 대한 참조(python 3.10)]

• class의 attribute를 가져오거나 얻을때 __getattr__와 __setattr__ 함수를 call한다. 예를 들어 Temp.att1 = 1이 실행되면 python의 __builtin__에 정의된 __setattr__를 call한다. 기본적으로 모든 Object들은 따로 재정의 하지않으면 python 내부에 정의된 함수들이 실행된다.

Reference

https://github.com/SkalskiP/ILearnDeepLearning.py