[baekjoon] 18237번 - 행렬 곱셈 순서 3(작성중)

2023.08.16 00:00

행렬 곱셈 순서 3

개요

크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.

예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.

AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.

같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.

행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.

입력

첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 200,000)이 주어진다.

둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 10,000)

항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.

출력

첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 $2^{63}-1$ 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 263-1보다 작거나 같다.

Hu & Shing 알고리즘 Part 1

1. Introduce

2. Partitioning a convex polygon

Fig 1.와 같이 육각형, n차 볼록 다각형이 주어지면, 다각형을 n-2개의 교차하지 않은 삼각형으로 분할 하는 경우의 수는 카탈란 수로 나타낼 수 있다. 그러므로 볼록 사각형은 2개의 경우의 수, 볼록 오각형은 5개의 경우의 수, 육각형은 14개의 경우의 수가 존재한다.

모든 다각형의 정점 $V_{i}$은 positive weight $w_{i}$를 가진다고 하자. 분할된 삼각형의 cost를 다음과 같이 정의 할수 있다. 삼각형의 cost는 3개의 정점들의 곱셈이고 분할된 다각형의 cost는 다각형의 모든 삼각형의 cost를 합한 것과 같다. 예를들어, Fig 1의 분할된 육각형의 cost는

\[w_{1}w_{2}w_{3} + w_{1}w_{3}w_{6} + w_{3}w_{4}w_{6} + w_{4}w_{5}w_{6}\]

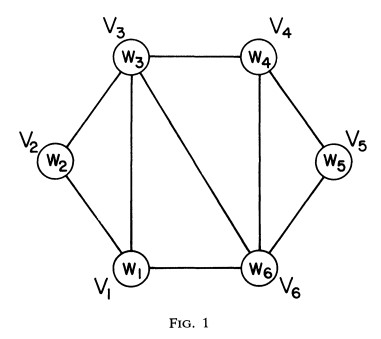
만약 $V_{3}$와 $V_{6}$를 잇는 대각선을 지우고 대신 $V_{1}$와 $V_{4}$를 잇는 대각선을 그리면 새롭게 분할된 공간의 cost는 다음과 같아진다.

\[w_{1}w_{2}w_{3} + w_{1}w_{3}w_{4} + w_{1}w_{4}w_{6} + w_{4}w_{5}w_{6}\]

여기서 $n - 1$개의 매트릭스의 곱셈 순서 문제를 n차원을 가지는 볼록 다각형의 분할 문제로 대응된다는 것을 보여줄것이다. 분할된 도형의 cost는 행렬의 곱셈에서 필요한 총 연산의 수이다. 간결성을 위해 n차원의 볼록 다각형을 n-gon으로 나타내고 분할된 n-gon을 교차되지 않은 n-2개의 삼각형으로 분할된 상태를 뜻한다.

n-gon의 한쪽을 시작으로 삼고 보통 Fig.1의 $V_{1}-V_{6}$와 같은 바닥과 직각으로 그린다. 이 사이드를 base로 부르고 모든 다른 사이드들은 시계 방향순서로 고려되어 진다. 그러므로, $V_{1}-V_{2}$이 첫번째 side가 되고, $V_{2}-V_{3}$은 두번째 side, $…$ 그리고 $V_{5}-V_{6}$이 마지막 6번째 사이드가 된다.

첫번쨰 사이드는 행렬 곱셈에서 첫번째 행렬 $M_{1}$으로 나타내고 모든 행렬의 결과 값은 (1)의 $M$으로 나타낸다. 행렬의 차원은 side의 양끝 정점의 weight과 연관되어 있다. 인접 행렬의 차원은 $w_{1} \times w_{2}, w_{2} \times w_{3}, … w_{n-1} \times w_{n}$와 같이 서로 호환 가능하기 떄문에 $w_{1}, w_{2}, …, w_{n}$와 같은 정점으로 사용되어 질 수 있다. n-gon의 분할 문제는 alphabetic tree of n-1 leaves에 대응 되거나 n-1개의 symbol을 가지는 parenthesis problem에 대응된다(Gardner[6]에서 예제를 보여준다). n-1개의 행렬 곱셈과 alphabetic binary tree 혹은 n-1개의 symbol을 가지는 parenthesis problem과 1대일 대응 하는 것은 쉽다. 행렬 연속 곱셈과 볼록 다각형의 분할 문제이 대응된다는 것을 직접적으로 보여줄 것이다.

$LEMMA \; 1.$

어떤 n-1개의 행렬 곱셈 순서 문제도 n-gon의 분할 문제와 대응 된다.

Proof. $w_{1} \times w_{2}, w_{2} \times w_{3}$ 차원을 가지는 2개의 행렬에서 곱셈하는 방법은 단 1개 밖에 없다. 이러한 사실은 삼각형은 더이상 분할이 불가능하다는 점과 대응된다. 총 곱셈 연산의 수는 $w_{1}w_{2}w_{3}$으로 삼각형의 3개의 정점의 weight를 곱한 것과 같다. 곱셈의 연산 결과 행렬은 $w_{1} \times w_{3}$이 된다. 3개의 행렬 곱셈에서 곱셈 연산 순서는 2가지의 경우의 수 $(M_{1} \times M_{2}) \times M_{3}$와 $M_{1} \times (M_{2} \times M_{3})$을 가지고 이것은 4-gon(사각형)의 2가지 분할 방법에 각각 대응 된다. $k \leqq n-2$인 k개의 행렬에서 이 lemma가 참이라고 가정하고 n - 1개의 행렬인 n-gon을 고려 해보자.

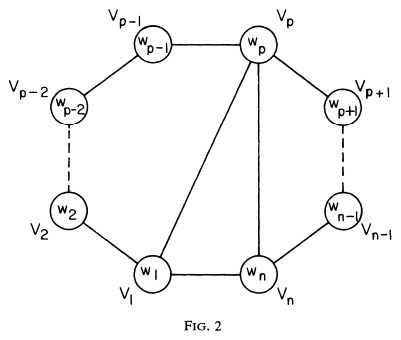
곱셈 순서는 다음과 같이 나타내어 진다.

\[M = (M_{1} \times M_{2} \times ... \times M_{p-1}) \times (M_{p} \times ... \times M_{n-1})\]

마지막 행렬은 다음 행렬의 차원들을 $(w_{1} \times w_{p})$, $(w_{p} \times w_{n})$ 곱함으로써 으로 얻어진다. n-gon의 분할에서 정점 $V_{1}$과 $V_{n}$을 지닌 삼각형의 세번째 정점을 $V_{p}$라고 하자. 다각형 $V_{1} - V_{2} - … - V_{p}$은 base $V_{1} - V_{p}$를 가지는 p side의 볼록 다각형이고 이 것의 분할은 결과로 $w_{1} \times w_{p}$의 행렬을 가지는 $M_{1}, …, M_{p - 1}$의 행렬 곱셈 순서와 대응된다. 유사하게 base $V_{p} - V_{n}$을 가지는 다각형 $V_{p} - V_{p+1} - … - V_{n}$의 분할은 행렬 연산의 결과로 $w_{p} \times w_{n}$의 행렬을 가지는 $M_{p}, …, M_{n - 1}$의 행렬 곱셈 순서와 대응된다.

그러므로 base를 $V_{1} - V_{n}$을 가지는 삼각형 $V_{1}V_{p}V_{n}$은 2개의 부분 곱셈의 곱으로 나타내어지고 그 결과로 $w_{1} \times w_{n}$의 차원을 가지는 행렬이 된다.

$LEMMA \; 2.$

다음의 행렬 연쇄 곱셈의 최소 연산 수는 동일 하다.
\[M_{1} \times M_{2} \times ... \times M_{n-2} \times M_{n-1}, \\ M_{n} \times M_{1} \times ... \times M_{n-3} \times M_{n-2}, \\ \vdots \\ M_{2} \times M_{3} \times ... \times M_{n-1} \times M_{n},\]

여기서 $M_{i}$은 $w_{i} \times w_{i + 1}$의 차원을 가지고 $w_{n+1} \equiv w_{1}$이다. 첫번째 수식의 행렬 연쇄 곱의 결과 행렬의 차원은 $w_{1} \times w_{n}$이 된다. 마지막 수식의 행렬 연쇄 곱의 결과 행렬의 차원은 $w_{2} \times w_{1}$이다. 결과 행렬의 차원은 다르지만 최적의 곱셈 순서에서 모든 case의 총 곱셈의 연산수는 동일하다.

Proof. n-1개의 행렬의 순환 순열(cyclic permutation)은 모두 똑같은 n-gon에 대응되고 그러므로 똑같은 최적 분할 방법을 공유한다. 이제부터는 우리는 분할 문제에만 집중할 것이다. 다각형 내부에 있는 대각선들을 호(arcs)라고 한다. 따라서 수식적으로 모든 분할은 n개의 변(side)과 n-3개의 호(arc)로 이루어진 n-2개의 삼각형으로 구성되어 있다. n각형의 분할에서 정점의 차수는 해당 정점으로 오는 호(arc)의 개수에 2개를 더한 것이다(모든 정점에는 변(side)가 2개 더 있기 때문에)

$LEMMA \; 3.$

n이 4이상인 경우 n각형의 어떤 분할에서도 적어도 2개의 삼각형이 있으며, 각각의 삼각형은 차수가 2인 정점을 가진다. (예시로 Fig 1.에서 삼각형 $V_{1}V_{2}V_{3}$은 차수가 2인 정점 $V_{2}$를 가진다.)

Proof. 어떤 n각형의 분할에서도 n개의 변과 n - 3의 호(arc)로 구성된 n-2개의 교차하지 않는 삼각형이 존재한다. 그리고 4이상인 어떤 n에서 3개의 변으로 구성된 삼각형은 존재 하지 않는다 (여기서 변은 다각형의 외부를 감싸는 base side(변)을 말함). x를 한개의 호(arc)와 2개의 변을 가지는 삼각형의 수라고 하고, y를 2개의 호(arc)와 1개의 변으로 이루어진 삼각형의 수 그리고 z를 3개의 호(arc)로 이루어진 삼각형의 수라고 하자. 1개의 호(arc)는 2개의 삼각형이 공유하므로 따라서 전체 호(arc)의 개수에 대한 다음의 식으로 나타낼수 있다.

\[x + 2y + 3z = 2(n - 3) \quad\; (4)\]

여기서, 전체 호(arc)의 개수는 n - 3개 이고 각각의 case의 삼각형이 지니는 호의 갯수를 모두 더한 것은 2개의 삼각형이 1개의 호(arc)를 공유하므로 2(n-3)과 같아 진다.

다각형은 n개의 변을 가지기 때문에 다음의 변에 대한 식으로 나타낼 수 있다.

\[2x + y = n \quad\; (5)\]

(4)와 (5)식으로 부터 n을 제거 하면 다음과 같은 식이 유도된다.

\[3x = 3z + 6\]

$z \geqq 0$ 이기 때문에 $x \geqq 2$을 얻고 1개의 호(arc)와 2개의 변을 가지는 삼각형의 수가 최소한 2개이상임을 알수있다. (n의 최소 조건인 사각형에서 분할시켜보면 이 조건을 만족하는 삼각형(x)이 딱 2개 나온다.)

$LEMMA \; 4.$

$P$ 와 $P’$ 둘다 n각형일때 각각의 대응되는 정점의 weight가 $w_{i} \leqq w’_{i}$을 만족한다고 할때, 다각형 $P$의 최적 분할의 cost는 다각형 $P’$의 최적 보다 작거나 같다.

Proof. 생략함

만약 $C(w_{1}, w_{2}, …, w_{k})$을 각 정점이 weight $w_{i}$을 가지는 n각형의 최적으로 분할하는 최소 cost를 뜻한다고 하면, Lemma 4에 의해 다음과 같이 표현 될 수 있다.

\[C(w_{1}, w_{2}, ..., w_{k}) \leqq C(w'_{1}, w'_{2}, ..., w'_{k}) \quad if \quad w_{i} \leqq w'_{i}\]

2개의 정점이 만약 호에의해 연결되어있거나 같은 변에서 인접해 있다면 2개의 정점은 최적 분할에 의해 연결되어 있다고 말할 수 있다. 논문의 나머지부분에서 정점들을 weight에 따라 정렬한 것을 나타내기 위해 $V_{1}, V_{2}, …, V_{n}$을 사용한다. 여기서 weight는 $w_{1} \leqq w_{2} \leqq … \leqq w_{n}$으로 정렬되어 있음. 설명을 쉽게 하기 위해 같은 weight를 가지는 정점들에 대한 우선순위 결정(tie-breaking) 규칙을 설명한다.

만약 2개 혹은 이상의 정점들의 weight가 가장 작은 weight인 $w_{1}$와 같다면 이러한 정점들 중 임의로 한개를 선택하여 정점 $V_{1}$으로 할 수 있다.

일단 정점 $V_{1}$이 선택되면 같은 무게의 정점들 사이의 추가적인 우선순위 결정은 $V_{1}$을 기준으로 시계방향으로 더 가까운 정점이 더 낮은 무게를 가진 것으로 간주하여 해결됩니다. 이런 우선순위 결정 규칙에 의해, $V_{1}$의 선택에 따라 $V_{1}, V_{2}, … , V_{n}$을 모호하지 않게 라벨링할 수 있다. 정점 $V_{i}$가 다른 정점인 $V_{j}$보다 작다는 것은 $V_{i} < V_{j}$으로 표기되며 $w_{i} < w_{j}$이거나 $w_{i} = w_{j}$이면 $i < j$으로 표기될 수 도 있다. 부분 다각형에서 다른 어떤 정점보다 작으면 부분 다각형에서 $V_{i}$가 가장 작다라고 말할 수 있다.

모든 정점이 라벨링되고, 만약 다음을 만족하면 호(arc) $V_{i} - V_{j}$는 다른 어떤 호(arc) $V_{p} - V_{q}$ 보다 작다고 정의할 수 있다.

\[min(i,\; j) < min(p,\; q) \quad or \quad \begin{cases} min(i, \; j) = min(p, \; q), \\ max(i, \; j) < max(p, \; q) \end{cases}\]

(예시로, 호 $V_{3} - V_{9}$은 호 $V_{4} - V_{5}$ 보다 작다.) ?? 4,5는 호가 아니라 변인데 뭔말인지 모르겟음

모든 n각형의 분할은 작은 것부터 큰 순으로 정렬될 수 있는 n-3개의 호(arc)를 가진다. 즉, 각각의 분할은 unique한 정렬 순서와 관련되어 있다. 만약 P에 연결된 호들의 정렬 순서가 Q에 연결된 호의 정렬 순서보다 사전적 순서보다 작으면 분할 P를 사전 순서상에서 분할 Q보다 작다라고 정의 할 수 있다.

한개 이상의 최적 분할이 있을때, 사전적순서에서 가장 작은 최적 분할을 뜻하는 l-optimum partition(i.e. lexcicographically-optimum partition) 을 사용하고 어떤 분할 최소 cost을 뜻하는 an optimum partition을 사용한다.

weight에서 정렬되지 않은 정점들을 나타내기 위해 $V_{a}, V_{b}, …$으로 표기하여 사용하고 $T_{ijk}$은 어떤 임의의 3개의 정점 $V_{i}, V_{j}$ and $V_{k}$의 weight 곱을 나타낸다고 하자.

THEOREM 1.

사전에 묘사된 $V_{1}, V_{2}, …$을 선택하는 모든 방법에서 최적 분할은 항상 $V_{1} - V_{2}$과 $V_{1} - V_{3}$을 포함한다. (여기서, $V_{1} - V_{2}$과 $V_{1} - V_{3}$은 호(arc)이거나 변이다.)

Proof. 이론은 귀납적으로 증명된다. 삼각형과 사각형의 최적 분할에서, 당연히 이론은 참이된다.

만약 이론이 모든 k각형 ($3 \leqq k \leqq n - 1$)에서 참이라고 가정하고 n각형의 최적 분할을 고려해보자.

Lemma 3으로 부터 어떤 최적 분할에서 적어도 2개의 정점은 2개의 차원을 가지는 것을 알수 있다. 이 두 정점을 $V_{i}$과 $V_{j}$라고 하고 이를 2가지 경우로 나눌 수 있다.

case (i) 2개의 정점중 하나 $V_{i}$ (혹은 $V_{j}$)은 n각형의 어떤 최적 분할에서 $V_{1}, V_{2}, V_{3}$가 아닌 경우 이 경우에서 $V_{i}$가 포함된 2개의 변을 제거하여 n-1각형을 얻을 수 있다. 이 n-1각형에서 $V_{1}, V_{2}, V_{3}$은 가장 작은 weight를 가지는 3개의 정점이 된다. 이 귀납 추정에 의해 $V_{1}$은 최적 분할에서 $V_{2}$와 $V_{3}$ 둘다에 연결되어 진다.

case (ii) (i)의 경우에서 보충을 하면, n각형의 모든 최적 분할에서 모든 차수가 2인 정점은 집합 {$V_{1}$, $V_{2}$, $V_{3}$}에서 나온다.(이 경우 모든 최적 분할에 차수가 2인 정점이 최대 3개 있다.) 다음 case (ii)의 하위 경우의 수가 3가지 있다.

case (ii) - (a) n각형의 어떤 최적 분할에서 $V_{i} = V_{2}$와 $V_{j} = V_{3}$ 일때, 즉 $V_{2}$와 $V_{3}$가 동시에 2차원을 가지는 상황이다. 이 경우에서 먼저 2개의 변을 가지는 $V_{2}$를 제거하고 n-1각형을 만든다. 귀납 가정에 따라 어떤 최적 분할에서 $V_{1}, \, V_{3}$은 연결될 수 밖에 없다. 만약 $V_{1} - V_{3}$이 호(arc)로 나타내어 지면 경우 (i)로 좁아지기 때문에 따라서 이는 $V_{1} - V_{3}$은 변으로 나타날 수 밖에 없다. 그리고 $V_{2}$을 n-1각형에 다시 붙이는 것으로 $V_{1}$, $V_{2}$와 $V_{3}$이 서로 인접하거나 혹은 $V_{1} - V_{3}$가 n각형의 변임을 보여준다. 전자의 경우, 증명은 완료되므로 $V_{1} - V_{3}$가 n각형의 변이라는 것을 가정한다. 유사하게 우리는 2개의 변을 가진 $V_{3}$을 제거함으로써 $V_{1}, V_{2}$가 n각형에서 변으로 연결되어 있음을 보여 줄 수 있다.

case (ii) - (b) n각형의 어떤 최적 분할에서 $V_{i} = V_{1}$와 $V_{j} = V_{2}$ 일때, 즉 $V_{1}$와 $V_{2}$가 동시에 2차원을 가지는 상황이다. 이 경우에서 먼저 $V_{1}$을 제거하고 n-1각형을 구성하면 여기서 $V_{2},\, V_{3}, \, V_{4}$은 가장 작은 weight를 가지는 3개의 정점이 된다. 귀납 가정에 따라, 최적 분할에서 $V_{2}$는 $V_{3}$와 $V_{4}$ 모두에 연결되어 진다. 만약 $V_{2} - V_{3}$ 혹은 $V_{2} - V_{4}$가 호(arc)로 나타나면 이는 경우 (i)로 축소된다. 그러므로 $V_{2} - V_{3}$와 $V_{2} - V_{4}$ 둘다 모두 n각형의 변이 될 수 밖에 없다. 비슷하게, $V_{2}$와 2개의 변을 제거해서 n-1각형을 만들어 $V_{1}, \, V_{3}, \, V_{4}$가 가장 작은 weight를 가지는 3개의 정점이 된다. 반복하면 $V_{1}$은 $V_{3}$와 $V_{4}$가 n각형의 변에 의해 연결되어 질 수 밖에 없다. 하지만 어떤 n각형($n \geqq 5$)에서 동시에 $V_{1}$과 $V_{2}$에 $V_{3}$와 $V_{4}$ 둘다 인접하는 것은 불가능 하기 때문에 즉, $V_{1}$과 $V_{2}$은 둘다 모두 어떤 n각형($n \geqq 5$)의 최적 분할에서 동시에 2차원을 가질 수 없게 된다.

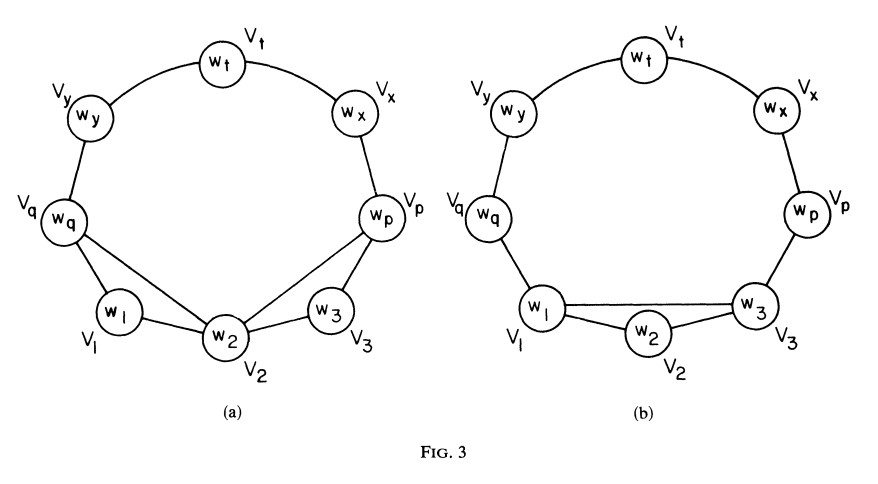
case (ii) - (c) n각형의 어떤 최적 분할에서 $V_{i} = V_{1}$와 $V_{j} = V_{3}$ 일때, (b)와 유사한 논증에 의해 $V_{2}$는 n각형에서 $V_{1}$과 $V_{3}$에 인접해야 함을 보일 수 있다. 이 상황은 Fig 3(a)에서 보여준다. 그다음 Fig 3(b)의 분할은 (a)보다 더 cost가 낮다.

\[T_{123} \leq T_{12q}\]

이고 Lemma 4에 의해 $C(w_{1}, w_{q}, w_{y}, w_{t}, w_{x}, w_{p}, w_{3}) \leqq C(w_{2}, w_{q}, w_{y}, w_{t}, w_{x}, w_{p}, w_{3})$ 이기 때문이다.

COROLLARY 1.

사전에 설명한 방식으로 $V_{1}, V_{2}, … $을 선택하는 모든 방법에서, l-optimum partition은 항상 $V_{1} - V_{2}$와 $V_{1} - V_{3}$을 포함한다.

Proof. Theorem 1과 l-optimum partition의 정의로 부터 증명됨.

일단 우리는 $V_{1} - V_{2}$와 $V_{1} - V_{3}$가 항상 l-optimum partition에 존재한다는 것을 알았다면, 이 사실을 (recursively)반복적으로 부분 partition에서 사용할 수 있다. 그러므로, 주어진 다각형의 l-optimum partition 을 찾기 위해서, 가장 작은 정점을 두번째로 작은 정점과 세번째로 작은 정점을 반복적으로 연결함으로써 다각형을 하위 다각형으로 분해 할 수 있다. 이때 각각의 하위 다각형의 가장 작은 정점이 두번째로 작은 정점과 세번째로 작은 정점 둘다 인접해야 한다.

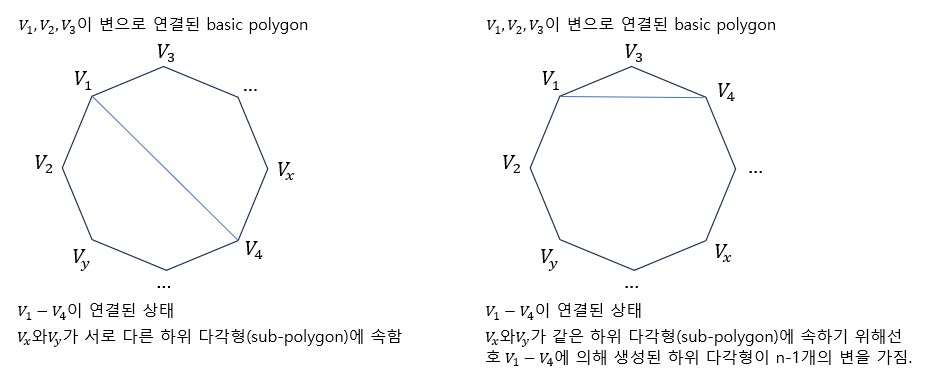
변에 의해 $V_{1}$가 $V_{2}와 V_{3}$에 인접해 있는 다각형을 기본 다각형(basic polygon)이라고 부를 것이다.

THEOREM 2. 이 기본 다각형(basic polygon)의 optimum partition에 $V_{2} - V_{3}$가 존재하기 위한 필요이지만 충분은 아닌 조건은 다음과 같다.

\[\frac{1}{w_{1}} + \frac{1}{w_{4}} \leqq \frac{1}{w_{2}} + \frac{1}{w_{3}}\]

게다가, 만약 $V_{2} - V_{3}$이 l-optimum partition에 존재하지 않으면, $V_{1}, V_{4}$들은 l-optimum partition 에서 항상 연결되어 있다. Proof. 만약 이 기본 다각형(basic polygon)의 l-optimum partition에서 $V_{2}$와 $V_{3}$이 연결되어 있지 않다면, $V_{1}$의 차수가 3보다 크거나 같다. $V_{p}$이 다각형에 있고 $V_{1}$과 $V_{p}$가 l-optimum partition에서 연결되어 있다고 가정하자. $V_{4}$은 $V_{1}, V_{2}$과 $V_{p}$을 포함하는 하위 다각형에 있거나 혹은 $V_{1}, V_{3}$과 $V_{p}$을 포함하는 하위 다각형에 있어야 한다. Corollary 1으로 부터 $V_{1}, V_{4}$은 하위 다각형의 l-optimum partition 에서 연결되어 있어야하고 이것 역시 기본 다각형의 l-optimum partition에서 $V_{1}, V_{4}$은 연결되어 있어야 한다.

만약, $V_{2}, V_{3}$ optimum partition에서 연결되어 있으면, $V_{2}$가 가장 작은 정점이고 $V_{4}$가 3번째로 작은 정점인 n-1 다각형이 된다. Theorem 1에 의해 $V_{2}, V_{4}$가 연결된 n-1 다각형의 optimum partition이 존재하게 된다. 그러므로 귀납 추론에 의해 Fig. 4에 그려진 기본 다각형(basic polygon)에서 $V_{4}$과 $V_{2}$이 인접해 있다는 것을 추론할 수 있게 된다.

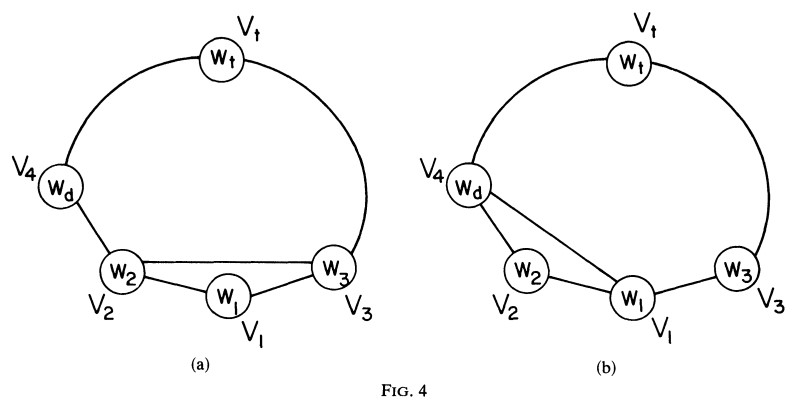
Fig. 4(a)에 그려진 partition의 cost는 다음과 같다. $T_{123} + C(w_{2}, w_{4}, ..., w_{t}, ... , w_{3}) \quad \; (7)$ 그리고 Fig. 4(b)에 그려진 partition의 cost도 다음과 같이 계산된다. $T_{124} + C(w_{1}, w_{4}, ..., w_{t}, ... , w_{3}) \quad \; (8)$

Lemma 4에 따라 다음과 같이 된다. $C(w_{1}, w_{4}, ... , w_{t}, ..., w_{3}) \leqq C(w_{2}, w_{4}, ... , w_{t}, ..., w_{3}) \quad \; (9)$

$V_{4}$와 $V_{3}$ 사이에 있는 정점들의 weight들은 시계방향으로 정렬되어 있기 때문에 모두 $w_{4}$보다 크거나 같기 때문에 오른쪽 변과 왼쪽 변 사이의 차이는 적어도 $T_{243} - T_{143}$가 된다. 그래서 (8)보다 (7)이 크지 않을 필요조건은 다음과 같이 2개가 된다.

\[T_{123} + T_{243} \leqq T_{124} + T_{134} \\ or \\ \frac{1}{w_{1}} + \frac{1}{w_{4}} \leqq \frac{1}{w_{2}} + \frac{1}{w_{3}}\]

LEMMA 5. n각형의 optimum partition에서 사전의 설$V_{x}, V_{y}, V_{z}, V_{w}$를 사각형의 정점이라고 하자($V_{x}$와 $V_{z}$는 사각형에서 인접하지 않는다.). 호 $V_{x} - V_{z}$가 존재할 필요 조건은 다음 (10)과 같다.

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{y}} + \frac{1}{w_{w}} \quad \; (10)\]

Proof. 호 $V_{x} - V_{z}$에 의해 분할된 사각형의 cost는 다음과 같다.

\[T_{xyz} + T_{xzw} = w_{x} w_{y} w_{z} + w_{x} w_{z} w_{w} = w_{x}w_{z}(w_{y} + w_{w})\quad \; (11)\]

또다른 경우인 호 $V_{y} - V_{w}$에 의해 분할된 사각형의 cost는 다음과 같다.

\[T_{xyw} + T_{yzw} = w_{x} w_{y} w_{w} + w_{y} w_{z} w_{w} = w_{y} w_{w} (w_{x} + w_{z})\quad \; (12)\]

(10)을 변형 다음과 같이 전개된다.

\[\frac{w_{x} + w_{z}}{ w_{x} w_{z}} \geqq \frac{w_{y} + w_{w}}{ w_{y} w_{w} } \\ w_{y} w_{w}(w_{x} + w_{z}) \geqq w_{x} w_{z}( w_{y} + w_{w} ) \\ (12) \geqq (11)\]

(10)으로 부터 $(11) \leqq (12)$을 얻는다.

(10)에서 엄격한 부등호가 성립하는 경우 필요 조건 역시 충분 조건이 된다. 만약 (10)에서 등호가 성립하는 경우, l-optimum partition에서 $V_{x} - V_{z}$가 존재할 충분한 조건은 $min(x, z) < min(y, w)$이다.

이 lemma 는 [3, lemma 1]의 일반화 이고 여기서 $V_{y}$는 가장 작은 정점이고 $V_{x}, V_{w}, V_{z}$들은 연속적으로 있는 정점들이며 $w_{w}$는 $w_{x}, w_{z}$ 둘다 보다 크다.

만약 partition에 있는 모든 사각형이 (10)을 만족한다면 partition은 stable 이라고 한다.

COROLLARY 2. optimum partition은 stable 하지만 stable partition은 optimum 하지 않을 수도 있다.

Proof. optimum partition은 stable하다는 사실은 Lemma 5로 부터 유도된다. Figure 5는 stable partition이 최적이 아닐수도 있다는 예를 보여준다.

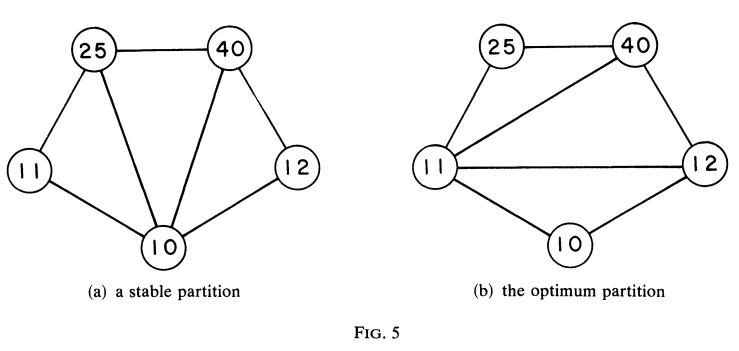
여기서 (a)의 부분 다각형인 사각형 10 - 11 - 25 - 40 에서 호 10 - 25로 분할되므로 $V_{x} - V_{z} = 10 - 25$이므로

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{y}} + \frac{1}{w_{w}} \\ \frac{1}{10} + \frac{1}{25} \geqq \frac{1}{11} + \frac{1}{40}\]

으로 성립하고 또다른 부븐 다각형인 10 - 25 - 40 - 12에서 호 10 - 40으로 분할되므로 $V_{x} - V_{z} = 10 - 40$이 된다.

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{y}} + \frac{1}{w_{w}} \\ \frac{1}{10} + \frac{1}{40} \geqq \frac{1}{11} + \frac{1}{25}\]

이 성립하므로 모든 사각형에서 (10)을 만족하므로 stable partition이라고 말할 수는 있지만 optimum partition은 아니다.

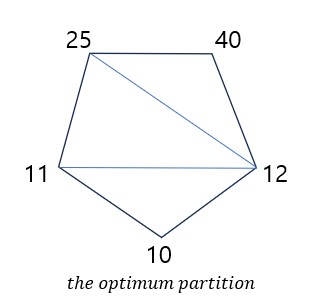
fig 5.(b)의 최적은 알고리즘을 돌리면 위와 같이 나오는데 예시가 틀린것 같아 그림을 바꿈..

여기서 (b)의 부분 다각형인 사각형 10 - 11 - 25 - 12 에서 호 11 - 12로 분할되므로 $V_{x} - V_{z} = 11 - 12$이므로

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{y}} + \frac{1}{w_{w}} \\ \frac{1}{11} + \frac{1}{12} \geqq \frac{1}{10} + \frac{1}{25}\]

으로 성립하고 또다른 부븐 다각형인 11 - 12 - 40 - 25에서 호 12 - 25으로 분할되므로 $V_{x} - V_{z} = 12 - 25$이 된다.

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{y}} + \frac{1}{w_{w}} \\ \frac{1}{12} + \frac{1}{25} \geqq \frac{1}{11} + \frac{1}{40}\]

으로 성립하고 각각의 사각형에 대해 $V_{y}$는 가장 작은 정점이 되며 $V_{w}$는 $V_{x}, V_{z}$보다 큰 정점이 된다. 또한 각각의 사각형에 대해 stable 하면서 optimum이 성립한다.

n각형의 어떠한 분할에서도 모든 호(arc)는 사각형에 한개씩만 존재한다. 사각형의 정점들을 $V_{x}, V_{y}, V_{z}, V_{w}$이라고 하고 $V_{x} - V{z}$을 사각형을 분할하는 호라고 하자. 이때 만약 (13)이나 (14)의 조건을 만족한다면 $V_{x} - V{z}$을 vertical arc라고 정의 한다.

\[min(w_{x}, w_{z}) < min(w_{y}, w_{w}) \quad \; (13) \\ min(w_{x}, w_{z}) = min(w_{y}, w_{w}), \quad max(w_{x},w_{z}) \leqq max(w_{y}, w_{w}) \quad \; (14)\]

만약 다음 조건 (15)를 만족한다면 $V_{x} - V_{z}$를 horizontal arc라고 정의 한다.

\[min(w_{x}, w_{z}) > min(w_{y}, w_{w}), \quad max(w_{x}, w_{z}) < max(w_{y}, w_{w}) \quad \; (15)\]

간결성을 위해 각각의 horizontal arcs와 vertical arcs를 h-arcs, v-arcs라고 지금 부터 명명한다.

COROLLARY 3. optimum partition에 있는 모든 호(arcs)들은 v-arcs 이거나 h-arcs이다.

Proof. $V_{x} - V_{z}$를 veritcal, horizontal 둘다 아니라고 하자. 여기에는 두 가지 경우가 존재한다.

Case 1. $min(w_{x}, w_{z}) = min(w_{y}, w_{w})$ 과 $max(w_{x}, w_{z}) > max(w_{y}, w_{w})$;

Case 2. $min(w_{x}, w_{z}) > min(w_{y}, w_{w})$ 과 $max(w_{x}, w_{z}) \geqq max(w_{y}, w_{w})$;

두 가지 경우 모두 다, Lemma 5의 부등식 (10)을 만족 하지 않는데 이는 분할이 stable하지 않고 optimum 하지 않는다라는 것을 암시 한다.

THEOREM 3. 다각형에서 인접하지 않는 임의의 두 정점을 $V_{x}$와 $V_{z}$이라 하고 $V_{w}$를 $V_{x}$에서 $V_{z}$가는 시계 방향으로 둘 사이의 가장 작은 정점이고 ($V_{w} \neq V_{x}, V_{w} \neq V_{z}$) $V_{y}$를 $V_{z}$에서 $V_{x}$가는 시계 방향으로 둘 사이의 가장 작은 정점이라고 하자 ($V_{y} \neq V_{x}, V_{y} \neq V_{z}$). 이것은 Fig. 6에서 보여준다. 여기서 일반성을 잃지 않고 $V_{x} < V_{z}$와 $V_{y} < V_{w}$라고 가정 할 수 있다.

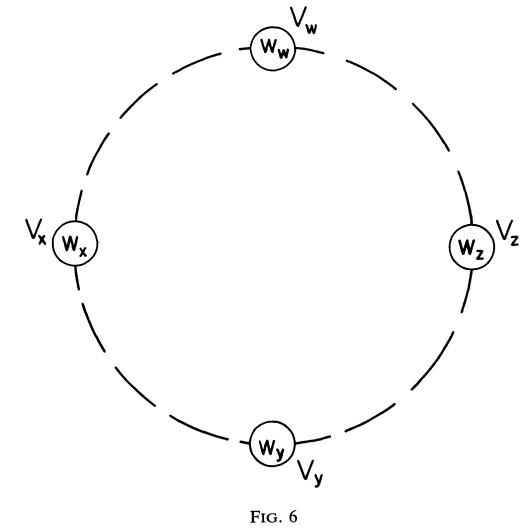
l-optimum partition에서 h-arcs로 $V_{x} - V_{z}$가 존재할 필요 조건은 다음과 같다.

\[w_{y} < w_{x} \leqq w_{z} < w_{w}\]

($V_{y}$와 $V_{w}$들의 위치가 서로 교환되어도 여전히 필요 조건을 만족한다.)

Proof. 이는 모순에 의해서 증명된다. 만약 $w_{x} \leqq w_{y}$이면 $w_{x}$는 가장 작은 weight인 $w_{1}$ 와 같아야만 하고 $V_{x} - V_{z}$는 절대 (15)를 만족하지 못한다. 그러므로 l-optimum partition에서 h-arcs로 $V_{x} - V{z}$가 존재하기 위해선, $w_{y} < w_{x} \leqq w_{z}$여야 한다. $V_{y}$는 V_{z}에서 V_{x}로 가는 시계 방향에서 가장 작은 정점이고 $V_{x} < V_{w}$이기 때문에 $V_{y} = V_{1}$이어야 한다.

일단 $V_{3} < V_{x} < V_{z}$라고 하자. Corollary 1.으로 부터 $V_{1} - V_{2}$와 $V_{1} - V{3}$ 둘다 l-optimum partition에 존재하고, 두 개의 호는 다각형을 하위 다각형으로 분할 한다. 만약 $V_{x}$와 $V_{y}$이 서로 다른 하위 다각형에 있으면, 두 정점은 l-optimum partition에서 연결될 수 없다. 일반성을 잃지 않고 다각형이 기본 다각형(basic polygon)이라고 가정할 수 있다.

기본 다각형(basic polygon)에서 $V_{2} - V_{3}$ 혹은 $V_{1} - V_{4}$ 중에 하나는 l-optimum partition에서 존재한다(Theorem 2.)

만약 $V_{2}, V_{3}$이 연결되어 있다면 $V_{x}$와 $V_{z}$ 둘 모두는 $V_{2}$를 가장 작은 정점으로 가지는 더작은 다각형에 포함된다.

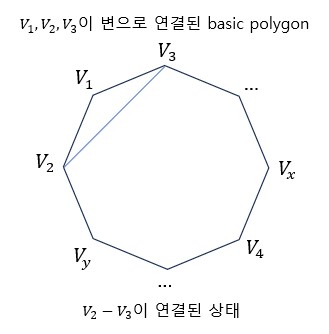
이를 똑같이 반복하여 만약 $V_{1}, V_{4}$이 연결되어 있다면 기본 다각형은 다시 2개의 하위 다각형으로 나뉘는데 이때 $V_{x}$와 $V_{z}$가 같은 하위 다각형에 속해야되고 이 하위 다각형이 최대 n-1개의 변을 가질 수 있다. (같은 하위 다각형에 속하지 않으면 $V_{x} - V_{z}$는 l-optimum partition에서 절대 존재 할 수 없다).

다각형의 크기가 연속적으로 감소하는 과정에서 $V_{x} - V_{z}$의 연결을 만드는 것이 절대로 불가능 하거나 혹은 기본 다각형(basic polygon)에서 $V_{x}$와 V_{z}가 2번쨰로 작거나 3번째로 작은 정점이 되는 것을 불가능하게 한다.

$V_{m}$을 이 기본 다각형에서 가장 작은 정점이라고 하자. $V_{x} - V_{z}$가 h-arcs로서 나타나기 위해서 $w_{x} > w_{m}$이어야 한다. Theorem 2로 부터 $V_{x} - V_{z}$(즉, $V_{2} - V_{3})$가 하위 다각형의 optimum partition에 존재할 필요 조건은 다음과 같다.

\[\frac{1}{w_{x}} + \frac{1}{w_{z}} \geqq \frac{1}{w_{m}} + \frac{1}{w_{w}}\]

이때 $w_{x} > w_{m}$ 이기 때문에 이 부등방정식은 오직 $w_{z} < w_{w}$일때만 유효하다.

COROLLARY 4. $V_{x} - V_{z}$이 l-optimum partition에서 h-arc로서 존재하는 약한 필요 조건은 다음과 같다.

\[V_{y} < V_{x} < V_{z} < V_{w}\]

Proof. 이는 Theorem 3으로부터 증명된다.

이 약한 필요 조건을 만족하는 어떤 호(arc)를 potential h-arc라고 부르자. $P$를 n각형에서 potential h-arcs들의 set이라고 하고 $H$를 l-optimum partition에서의 h-arcs의 set이라 하면 우리는 $P \supseteq H$ 라는 결과를 얻고 여기서 포함은 적절할 수도 있다.??

COROLLARY 5. 다각형에서 $V_{w}$을 가장 큰 정점이라고 하고 $V_{x}$와 $V_{z}$가 이웃한 정점이라고 하자. 만약 $V_{y} < V_{x}$와 $V_{y} < V_{z}$을 만족하는 $V_{y}$가 존재한다고 하면 $V_{x} - V_{z}$는 potetial h-arc가 된다.

Proof. 이는 Corollary 4으로 부터 직접 증명되고 여기서 $V_{x}$와 $V_{z}$ 사이에는 오직 한개의 정점만 존재한다.

분할에서 두 개의 호(arc)가 모두 동시에 존재한다면 이 두 개의 호(arc)들은 compatible하다고 부른다. 모든 정점의 weight에서 중복이 없다고 가정할때 여기서 중복이 없는 $(n-1)!$개의 permutation이 존재한다. 예를 들어 Fig. 5(a)의 weight들 10, 11, 25, 40, 12를 $w_{1}, w_{2}, w_{3}, w_{4}, w_{5}$의 permutation에 대응한다(여기서 $w_{1} < w_{2} < w_{3} < w_{4} < w_{5}$ 이다). 여기에는 똑같은 permutation을 갖는 수 많은 value들이 많이 존재한다. 예를 들어 1, 16, 34, 77, 29 역시 $w_{1}, w_{2}, w_{3}, w_{4}, w_{5}$ 에 대응 되지만 이 숫자 집합의 optimum partition은 10, 11, 25, 40, 12와는 다르다.

하지만 똑같은 weight permutation 조합을 가지는 모든 n각형에 있는 모든 potential h-arcs들은 compatible 하다. 이 주목할만한 사실을 Theorem 4으로 지정한다.

THEOREM 4. 모든 potential h-arcs들은 compatible 하다.

Proof. 이론은 모순에 의해 증명된다.

$V_{x}, V_{y}, V_{z} \; and \; V_{w}$를 Theorem 3에 설명된 4개의 정점이라고 하자. 그러므로, 우리는 $V_{y} < V_{x} < V_{z} < V_{w}$와 $V_{x} - V_{z}$이 potential h-arc 라는 사실을 얻는다. Fig. 7에서 표시된 것처럼 $V_{p} - V_{q}$를 $V_{x} - V_{z}$와는 compatible하지 않는 potential h-arc라고 하자 (동시에 존재할 수 없음). 일반성을 잃지 않고 $V_{p} < V_{q}$라고 가정할 수 있다(증명은 $V_{q} < V_{p}$인 경우와 유사하다). $V_{w}$는 $V_{x}$와 $V_{z}$ 사이의 시계 방향으로 존재하는 가장 작은 정점이기 때문에 $V_{z} < V_{w} < V_{q}$라는 사실을 얻는다. 그러므로, $V_{y} < V_{p} < V_{z} < V_{q}$ 혹은 $V_{y} < V_{z} < V_{p} < V_{q}$라는 두개의 정보 중의 하나를 얻을 수 있고 두 가지 경우 모두다 Corollary 4를 침범하기 떄문에 $V_{p} - V_{q}$은 potential h-arc로 존재할 수 없다.

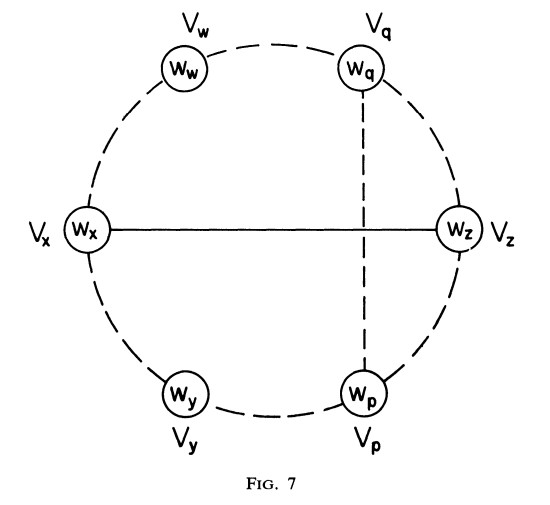
potential h-arc인 $V_{x} - V_{z}$은 항상 n각형을 2개의 하위 다각형으로 분할하고 이 하위 다각형들 중 하나는 다음의 특성을 가진다. 이 하위 다각형이 가지는 $V_{x}$와 $V_{z}$을 제외한 모든 정점들의 weight들은 $max(w_{x}, w_{z})$보다 작지 않다. 이 하위 다각형을 $V_{x} - V_{z}$의 upper subpolygon으로 부른다. 예를 들어 Fig. 7에서 $V_{x} - … - V_{w} - … - V_{z}$이 $V_{x} - V_{z}$의 upper subpolygon이다.

Coorollary 4와 Theorem 4을 사용하여 다각형의 모든 potential h-arcs를 생성할 수 있다.

$V_{x} - V_{z}$를 Corollary 5에서 정의된 호(arc)라고 하자, 즉, $V_{1} < V_{x} < V_{z} < V_{w}$이다. 호 $V_{x} - V_{z}$은 potential h-arc이고 다각형에 있는 모든 다른 potential h-arcs들과 compatible하다.

게다가, 이 upper subpolygon에서 다른 potential h-arc는 존재 하지 않는다. 여기서 $V_{w}$을 제거하여 얻어지는 n-1각형을 고려해보자. 이 n-1각형에서 $V_{w’}$은 가장 큰 정점이고 $V_{x’}$와 $V_{z’}$을 이웃으로 가지고 있다고 하자. 여기서 $V_{1} < V_{x’} < V_{z’} < V_{w’}$이다.

그러면 $V_{x’} - V_{z’}$은 다시 n각형에서 모든 다른 potential h-arcs들과 compatible한 potential h-arc가 되고 생성되지 않은 이것의 upper subpolygon에 또 다른 potential h-arc는 존재 하지 않게된다.

이는 심지어 $V_{w}$가 $V_{x’} - V_{z’}$의 upper subpolygon에 속해도 성립한다. 먄약 가장 큰 정점을 자르는 과정을 반복하면 모든 호(arc)들이 Corollary 4를 만족하는 $P$ set을 얻을 수 있다. l-optimum partition의 h-arcs는 이 호(arc)들의 부분 집합이 된다.

가장 큰 정점을 자르는 과정은 $O(n)$의 시간 복잡도를 가지는 알고리즘으로 만들 수 있다. 이 알고리즘은 one-sweep algorithm이라고 부를 것이다. 이 알고리즘의 결과는 n-3개 arcs의 set $S$이다. $S$는 알고리즘을 시작할때 비어있는 상태이다.

The one-sweep algorithm은 $V_{1}$이라고 부르는 가장 작은 정점으로 부터 시작하고 다각형을 시계 방향으로 순회 하고 다음의 규칙을 따르는 스택에 정점의 weight를 넣는다(아마 $w_{1}$이 스택의 가장 아래에 위치 할 것이다).

(a) 스택의 top에 있는 원소를 $V_{t}$라고 하면, $V_{t-1}$는 $V_{t}$ 바로 아래에 있는 원소가 되고 $V_{c}$는 스택에 추가될 원소라고 하자. 만약 스택에 2개 이상의 정점이 있고 $w_{t} > w_{c}$ 이면, $S$에 $V_{t-1} - V_{c}$를 추가하고 스택에서 $V_{t}$를 pop한다. 만약 스택에 1개의 정점만 있거나 $w_{t} \leqq w_{c}$이면 스택에 $w_{c}$를 넣는다. 위의 두 과정을 스택에 n번쨰 정점이 push될때까지 반복한다.
(b) 만약 스택에 4개이상의 정점이 존재하면, $S$ 에 $V_{t-1} - V_{1}$을 추가하고, $V_{t}$를 스택에서 꺼내고 이 과정을 멈출떄까지 반복한다.

최대 정점의 두 이웃 정점보다 작거나 같은 가중치를 가진 가장 작은 정점의 존재 여부를 확인하지 않기 때문에, 즉, Corollary 4에서의 $V_{y}$ 정점의 존재 여부를 확인하지 않기 때문에, 알고리즘에 의해 생성된 모든 n-3 개의 arc가 potential h-arc은 아니다. 하지만, $one-sweep algorithm$은 항상 n-3개의 arc set $S$를 생성한다. 이 set $S$는 모든 potential h-arcs의 set인 $P$를 포함한다. 역시 set $P$ 또한 n각형의 l-optimum partition에서의 모든 h-arcs의 set인 $H$를 포함한다. 즉, $S \supseteq P \supseteq H$가 된다.

예를 들어, 만약 시계방향으로 n각형 주변의 정점의 weight들을 $w_{1}, w_{2}, …, w_{n}$ 이라 하면, 여기서 $w_{1} \leqq w_{2} \leqq … \leqq w_{n}$, n각형에 Corollary 4를 만족하는 호(arc)가 없고 그러므로 이 n각형에 potential h-arcs가 없게된다.

one-sweep algorithm은 여전히 n각형의 n-3개의 호들을 생성하지만 생성된 호(arc)들 중에는 potential h-arc는 없다.

3. Conclusion

이 논문에서는 다각형을 분할하는 문제에 대한 몇몇개의 정리(theorem)를 설명했다. 이 정리들 중 일부는 어떤 볼록 n각형의 optimum partition을 나타내는 특성이며, 다른 몇가지는 유일한 가장작은 사전순의 optimum partition 이다. 이 정리들을 기반한 near-optimum partition을 찾는 $O(n)$의 알고리즘은 개발되었다[12]. 휴리스틱한 알고리즘에 의해 생성된 partition의 비용은 절대 $1 \cdot 155 C_{opt}$를 넘지 않고, 여기서 $C_{opt}$는 다각형을 최적으로 분할하는 비용이다. 사전순으로 가장작은 유일한 optimum partition을 찾는 $O(n \log n)$의 알고리즘은 Part 2에서 설명한다.

Hu & Shing 알고리즘 Part 2

1. Introduction

이 논문[6]의 Part 1에서 우리는 행렬 연속 곰셉 문제를 최적 분할 문제로 변환하고 볼록 n 각형의 최적 분할에 대한 몇가지 정리를 설명했다. Part 1에서 몇가지 정리들은 여기서 보충되고 다시 설명될 것이다.

*THEOTREM 1. * (Part 1에서 사전 설명된 것처럼)$V_{1}, V_{2}, …$의 모든 선택에서, 만약 n각형의 정점의 weight들이 다음의 조건을 만족한다면, 여기서 $3 \leqq k \leqq n$

\[w_{1} = w_{2} = ... = w_{k} < w_{k+1} \leqq ... \leqq w_{n}\]

그러면 모든 n각형의 optimum partition은 $V_{1} - V_{2} - … - V_{k}$인 k각형을 포함한다. 게다가, 만약 위의 조건에서 $k=2$이면 즉, $w_{1} = w_{2} < w_{3} \leqq w_{4} \leqq … \leqq w_{n}$, n각형의 모든 optimum partition은 $w_{3}$가 같은 weight를 가지는 어떤 정점 $V_{p}$에 대한 삼각형 $V_{1}V_{2}V_{p}$를 포함해야만 한다. 여기서 만약 $w_{1} = w_{2} < w_{3} < w_{4} \leqq … \leqq w_{n}$이라면 모든 optimum partition 은 유일하게 $V_{3}$을 선택할 수 밖에 없기 때문에 삼각형 $V_{1}V_{2}V_{3}$를 포함해야만 한다. 지금 여기서 3개 이상이나 그 이상의 정점들이 $w_{1}$과 같아도 우리는 n각형을 정리 1의 첫번째 부분의 k각형을 형성함으로써 하위 다각형으로 분해가 가능하다. 이 k각형의 모든 정점들은 같은 weight를 가지기 떄문에 k각형의 분할은 유일하지 않고 임의적이다.(어떤 방향으로 나눠도 weight가 같기때문에 같은 값이 나옴) $w_{1}$과 같은 weight를 정점을 2개 가진 어떤 하위 다각형에서, 정리 1의 2번째 파트를 적용할 수 있고 더 작은 하위 다각형으로 분해 할 수 있다. 그러므로 우리는 오직 하나의 $V_{1}$을 가진 즉, $w_{1}$과 같은 weight를 가진 정점이 오직 1개 일때만 고려하면 된다.

위의 정리 때문에, Part 1의 정리 1과 정리 3은 다음과 같이 일반화 할 수 있다.

THEOREM 2. (Part 1에서 설명된) $V_{1}, V_{2}, …$을 선택하는 모든 방법에서, 만약 정점들의 weight가 다음 조건을 만족한다면, n각형의 모든 optimum partition에는 $V_{1} - V_{2}$와 $V_{1} - V_{3}$가 존재한다.

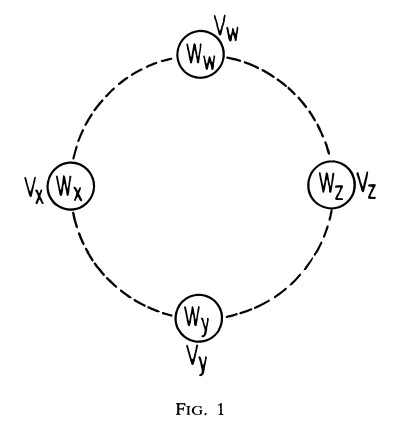
\[w_{1} < w_{2} \leqq w_{3} \leqq ... \leqq w_{n}\]

THEOREM 3. 다각형에서 인접하지 않는 임의의 두 정점을 $V_{x}$, $V_{z}$라고 하고 $V_{w}$을 시계 방향으로 $V_{x}$에서 $V_{z}$에 있는 가장 작은 정점이고 $(V_{w} \neq V_{x}, \; V_{w} \neq V_{z})$ $V_{y}$을 시계 방향으로 $V_{z}$에서 $V_{x}$에 존재하는 가장 작은 정점이라고 하자 $(V_{y} \neq V_{x}, \; V_{y} \neq V_{z})$. 이것은 Fig 1.에서 그림으로 보여준다.

$V_{x} < V_{z}$이고 $V_{y} < V_{w}$라고 가정한다. $V_{x} - V{z}$가 어떤 optimum partition의 h-arc로서 존재할 필요 조건은 다음과 같다.

\[w_{y} < w_{x} \leqq w_{z} < w_{w}\]

우리는 l-optimum partition을 the lexicographically smallest optimum partition의 의미로 사용한다. 지금부터 유일한 l-optimum partition을 찾는 알고리즘에 대해 설명한다.

이전 논문인 Part 1과 똑같은 notation(기호)를 사용하여 유일하게 라벨링된 n각형을 가정할 수 있다. partition은 fan으로 부른다. 이 fan은 다각형에서 가장 작은 정점과 모든 다른 정점이 연결된 오직 v-arc로만 구성된다. 다각형 $V_{1} - V_{b} - V_{c} - … - V_{n}$의 fan은 Fan $(w_{1} | w_{b}, w_{c}, … , w_{n})$으로 표기한다. 가장 작은 정점인 $V_{1}$을 fan의 중점이라고 부른다.

만약 어떤 정점의 이웃한 양 옆의 정점들 보다 크면 이 정점을 local maximum 정점으로 정의하고 반대로 양 옆의 정점들 보다 작으면 이 정점을 local minimum 정점으로 정의한다.

만약 오직 하나의 local maximum과 오직 하나의 local minimum만 존재하면 이 다각형을 monotone 다각형으로 부른다.

monotone 다각형의 l-optimum partition을 찾기 위한 $O(n)$의 알고리즘을 주고 이후 일반적인 볼록 다각형의 l-optimum partition을 찾는 $O(n \log n)$의 알고리즘을 줄 것이다.

2. Monotone basic polygon

이 섹션에서 monotone 다각형의 optimum partition을 다룰 것이다. 정리 1과 정리 2로 부터 우리는 오직 monotone basic polygon만 다루면 된다. (이 다각형은 $V_{1}$가 변(side)에 의해 $V_{2}, V_{3}$와 인접한 basic polygon이라고 불리는 다각형이다.) 이 특수한 경우의 이해는 일반적인 볼록 다각형의 optimum partition을 찾는데에 필수적이다.

monotone basic n각형인 $V_{1} - V_{2} - V_{c} - … - V_{3}$을 고려해보자, 이 다각형의 fan은 $Fn (w_{1}|w_{2}, w_{c}, … , w_{3})$ 으로 표시 되고 여기서 가장 작은 정점인 $V_{1}$ 은 fan의 중심이 된다.

fan의 정의는 또한 하위 다각형에도 잘 적용된다. 예를 들어, 만약 basic n각형에서 $V_{2}, V_{3}$이 연결되고 하위 n-1각형에서 $V_{2}$는 가장 작은 정점이 된다. n-1각형에서 모든 정점과 $V_{2}$의 연결로 인해 생성된 partition은 $Fan(w_{2} | w_{c}, … , w_{3})$으로 표시한다.

LEMMA 1. 만약 n각형의 l-optimum partition에서 어떠한 potential h-arc도 나타나지 않는다면, l-optimum partition은 n각형의 fan이 될 수 밖에 없다.

Proof. 생략됨. [7]에서 자세한 사항을 보면됨.

potential h-arc는 다각형을 두 부분으로 나눌 것이고, 이 나눠진 부분에서 큰 정점을 포함하는 하위 다각형을 upper subpolygon이라고 부른다. 어떤 n각형의 두 potential h-arcs를 각각 $V_{i} - V_{j}$와 $V_{p} - V_{q}$라고 하자.

만약 $V_{i} - V_{j}$ 의 upper subpolygon 이 $V_{p} - V_{q}$ 의 upper subpolygon을 포함한다면, $V_{p} - P_{q}$는 $V_{i} - V_{j}$ 보다 위에 있다 혹은 높다라고 말할 수 있다.

$P$를 monotone basic n각형에서의 모든 potential h-arcs의 set이라고 하자. $P$는 최대 n-3개의 arcs를 갖는다.

LEMMA 2. $P$에 있는 어떤 2개의 호를 $V_{i} - V_{j}$와 $V_{p} - V_{q}$라고 할때 둘 중의 한 호는 다른 호보다 높게 있다( $V_{i} - V_{j} > V_{p} - V_{q} \quad or \quad V_{i} - V_{j} < V_{p} - V_{q}$ ).

Proof. [7]에서 자세한 내용이 있다. 논문에서는 생략되어있지만 호(arc)끼리는 교차되지 않으므로 항상 어떤 호가 상위에 있을 수 밖에 없다.

생략된 내용

모순에 의해 증명이 가능하다. 이 Lemma 2 를 만족하지 않는 P에 속한 2개의 호를 $V_{i}-V_{j}$, $V_{p}-V_{q}$라고 하자

$V_{i}-V_{j}$와 $V_{p} - V_{q}$의 subpolygon들의 교집합이 공집합이거나 서로 일부만을 공유하고 있어야 한다. 그렇

우리는 local maximum을 항상 위에 local minimum을 항상 아래에 그리는 방법으로 monotone basic polygon을 그림으로 그려서 potential h-arcs의 순서를 보여줄 수 있다. 만약 $V_{i} - V_{j}$ 의 upper subpolygon이 $V_{p} - V_{q}$ 의 upper subpolygon을 포함한다면 potential h-arc인 $V_{p} - V_{q}$는 다른 potential h-arc인 $V_{i} - V_{j}$보다 항상 물리적으로 위에 있다.

monotone의 특성과 upper subpolygon의 정의로 부터, 만약 $V_{p} - V_{q}$가 $V_{i} - V_{j}$보다 위에 있다면 $max(w_{i}, W_{j}) < min (w_{p}, w_{q})$임을 알 수 있다.

Fig 2.에 나타난 monotone basic n각형을 고려 해보자. $V_{n}$은 local maximum 정점이 되고 $V_{p} - V_{q}, \; V_{i} - V_{j} $는 monotone basic n각형의 potential h-arcs가 된다.

2개의 potential h-arcs $V_{p} - V_{q}$와 $V_{i} - V_{j}$ 그리고 시계 방향으로 $V_{i}$에서 $V_{p}$으로 있고 $V_{q}$에서 $V_{i}$에 있는 n각형의 변들에 의해 생성된 subpolygon $V_{i} - … - V_{p} - V_{q} - … - V_{j}$은 간결성을 위해 $V_{p} - V_{q}$ 아래 범위와 $V_{i} - V_{j}$ 위 범위 라고 말하거나 간단하게 $V_{i} - V_{j}$와 $V_{p} - V_{q}$사이의 subpolygon이라고 말한다.

LEMMA 3. monotone basic n각형에서 2개의 potential h-arc에 의해 범위가 정해진 어떤 subpolygon은 그자체로 monotone polygon이 된다.

Proof. [7]에 자세한 내용이 있음.

LEMMA 4. monotone basic n각형에서 아래 위로 있는 potential h-arcs에 의해 범위가 정해진 subpolygon의 어떤 potential h-arc 또한 monotone basic n각형의 potential h-arc가 된다.

Proof. [7]에 자세한 내용이 있음.

지금 부터 우리가 다뤘던 것을 요약하려고 한다. monotone basic n각형의 l-optimum partition에 h-arc가 없다면, l-optimum partition은 fan 이어야 한다. 다른의미로, l-optimum partition에 있는 h-arcs들은 모두 어떤하나가 다른 것 위에 있는 층으로 쌓여있다. local maximum $V_{n}$과 local minimum $V_{1}$을 2개의 h-arcs에 의해 없어진다면 monotone basic n각형의 l-optimum partition은 하나 혹은 이상의 monotone subpolygon을 포함 할 것이다. 2개의 h-arc에 의해 범위가 정해지거나 각각의 이러한 monotone subpolygon의 l-optimum partition은 fan이 된다.

그러면 monotone basic polygon의 l-optimum partition을 찾는 과정에서 오직 한개이거나 그 이상의 potential h-arcs를 포함하는 이러한 partition을 고려하기만 되거나 2개의 potential h-arcs의 사이에 있는 각 subpolygon들의 fan으로 분할하면 된다.

이 monotone basic n각형에 적어도 제거되지 않는 n-3개의 potential h-arc가 있기 때문에, 적어도 $2^{n-3}$개의 분할이 있고 이러한 모든 분할은 partition이 포함하는 nondegenerated potential h-arc에 의해 n-2개의 class로 나눌 수 있다.

이러한 class들은 $H_{0}, H_{1}, … , H_{n-3}$으로 표기된다. 여기서 $H$ 아래 첨자는 해당 class의 각 partition에 있는 nondegenerated potential h-arcs의 개수를 나타낸다.

$H_{0}$의 partition에는 potential h-arc가 없다. 그러므로 class는 오직 한개의 partition으로 구성되고 fan은 다음과 같이 된다.

\[Fan(w_{1} | w_{2}, ... , w_{3})\]

class $H_{1}$에서 각 partition은 하나의 nondegenerated potential h-arc을 가진다. 일단 potential h-arc가 정해지면, 나머지 부분의 호(arc)들은 vertical arc로 이루어져 2개의 부분 다각형마다 하나의 팬을 형성한다.

monotone basic polygon의 $H_{1}$의 2개의 전형적인 분할을 Fig. 3에 보여준다. Fig. 3(a)에는 한개의 nondegenerated potential h-arc인 $V_{c} - V_{i}(V_{c} < V_{i}$가 존재한다.

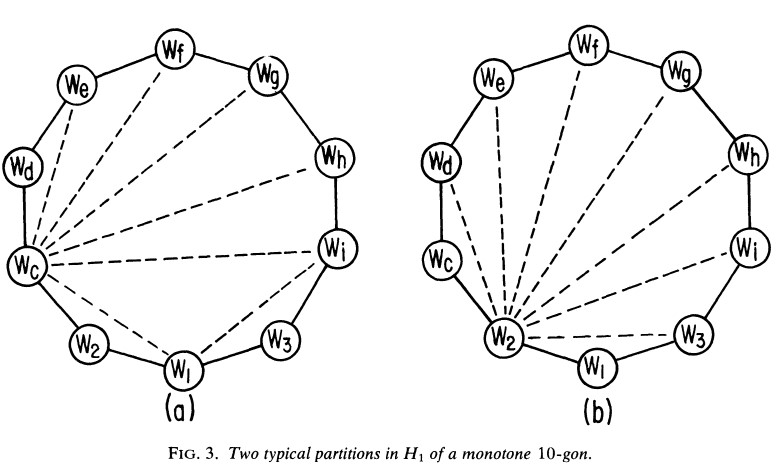
upper subpolygon의 fan은 다음과 같다.

\[Fan(w_{c} | w_{d}, ... , w_{i})\]

lower subpolygon의 fan은 다음과 같다.

\[Fan(w_{1} | w_{2}, w_{c}, w_{i}, w_{3})\]

Fig. 3(b)은 한개의 potential h-arc인 $V_{2} - V_{3}$가 있고 이때 upper subpolygon의 fan은 $Fan(w_{2} | w_{c}, … , w_{3}$가 되고 lower subpolygon은 degenerated fan으로 삼각형이다.

Fig. 3(b)에서 분할의 cost는 다음과 같다.

\[w_{1}w_{2}w_{3} + w_{2} ( w_{c} w_{d} + w_{d} w_{e} + w_{e} w_{f} + w_{f} w_{g} + w_{g} w_{h} + w_{h} w_{i} + w_{i} w_{3}) \\ \quad \quad \quad \quad \quad \quad \quad = w_{1} w_{2} w_{3} + w_{2}(w_{c}:w_{3}) \quad \; (1)\]

여기서 $w_{c}:w_{3}$ 는 $w_{c}$부터 $w_{3}$까지 시계 방향으로 인접한 원소 곱의 합을 간략하게 나타낸 기호이다.

Fig. 3에 표시된 다각형의 $H_{0}$의 cost를 표시하면 다음과 같다.

\[Fan (w_{1} | w_{2}, ... , w_{3}) = w_{1}(w_{2} : w_{3}) \quad \; (2)\]

(1)이 (2)보다 작을 조건은 다음과 같다.

\[\begin{split} (1) &< (2) \\ w_{1} w_{2} w_{3} + w_{2}(w_{c}:w_{3}) &< w_{1}(w_{2} : w_{3}) \\ w_{2}(w_{c}:w_{3}) &< w_{1}(w_{2} : w_{3}) - w_{1} w_{2} w_{3} \\ w_{2}(w_{c}:w_{3}) &< w_{1}((w_{2} : w_{3}) - w_{2} w_{3}) \\ \frac{w_{2} \cdot (w_{c} : w_{3})}{(w_{2}: w_{3}) - w_{2} \cdot w_{3}} &< w_{1} \end{split}\]

유사하게도 Fig. 3(a)에서 $H_{0}$보다 작을 조건은 다음과 같이 전개된다.

\[\begin{split} H_{0} \; cost &= Fan(w_{1} | w_{2}, ... , w_{3}) \\ &= w_{1} (w_{2}w_{c} + w_{c}w_{d} + w_{d}w_{e} + w_{e}w_{f} + w_{f}w_{g} + w_{g}w_{h} + w_{h}w_{i} + w_{i}w_{3}) \\ Fig.\,3(a) \; cost &= Fan(w_{c} | w_{d}, ... , w_{i}) + w_{c}w_{1}w_{2} + w_{1}w_{3} w_{i} + w_{c}w_{i} w_{1} \end{split}\] \[\require{cancel} Fig.\,3(a) \; cost < H_{0} \; cost \\ w_{c}(w_{d}:w_{i}) + \cancel{w_{1}w_{2}w_{c} + w_{1}w_{i} w_{3}} + w_{1}w_{i} w_{c} < w_{1}(w_{c}:w_{i}) + \cancel{w_{1}w_{2}w_{c} + w_{1}w_{i}w_{3}} \\ w_{c}(w_{d}:w_{i}) < w_{1}(w_{c}:w_{i}) - w_{1}w_{i} w_{c} \\ \frac{w_{c}(w_{c}:w_{i})}{w_{d}:w_{i} - w_{i}w_{c}} < w_{1} \quad \; (3)\]

만약 최소 cost를 가진 모든 분할 사이에서 사전적순서에서 가장 작은 분할이면 어떤 클래스(혹은 여러 클래스)의 분할들 중에 l-optimal이라고 말할 수 있다. 그러므로, 이 l-optimum 분할은 $H_{0}, H_{1}, … , H_{n-3}$ 클래스들의 모든 분할중에서 l-optimal이다.

Fig. 4에 보여진것처럼 오직 하나의 potential h-arc인 $V_{i} - V_{k}$를 포함하는 클래스들 $H_{1}, H_{2}, … , H_{n-3}$의 모든 분할들 사이에 있는 l-optimal partition이 있다고 가정하자.

만약 이 l-optimal이 $H_{0}$의 fan보다 cost가 적다면, 이 분할(optimal)은 monotone basic n각형의 l-optimum partition이 될것이다.

오직 한개의 h-arc인 $V_{i} - V_{k}$을 가진 분할이 $H_{0}$보다 비용이 작은 조건은 다음과 같다.

\[\frac{w_{i} \cdot (w_{j}:w_{k})}{(w_{i}:w_{k}) - w_{i} \cdot w_{k}} < w_{1} \quad \; if \; w_{i} \leqq w_{k} \\ or \\ \frac{w_{k} \cdot (w_{i}:w_{g})}{(w_{i}:w_{k}) - w_{i} \cdot w_{k}} < w_{1} \quad \; if \; w_{k} < w_{i} \\\]

위의 2개의 부등식을 조합해 다음과 같은 결과를 얻을 수 있다.

\[\frac{C(w_{i}, ... , w_{k})}{(w_{i}:w_{k}) - w_{i} \cdot w_{k}} < w_{1} \quad \; (4)\]

여기서 $C(w_{i}, … , w_{k})$ subpolygon $w_{i} - w_{j} - … - w_{g} - w_{k}$의 optimum partition의 비용을 나타내고 이경우 fan의 비용과 동일하다.

3. The convex polygon

4. Conclusion

Reference

https://en.wikipedia.org/wiki/Matrix_chain_multiplication https://github.com/junodeveloper/Hu-Shing

Share on

Twitter Facebook LinkedIn

Jean Valjean