[baekjoon] 28306번 - 제곱수 순열(나중에 풀 문제)

제곱수 순열

문제

1부터 N까지의 정수를 한번씩만 사용하여 다음 조건을 만족하는 수열 $A_{1}, A_{2}, …, A_{N}$을 출력하시오

• $A_{i} + A_{i+1}$은 제곱수이다. ($1 \le i < N$)

입력

총 $T$개의 테스트 케이스가 입력으로 주어지며, 첫 번째 줄에 $T$가 주어진다.

그 다음 줄부터 각 테스트 케이스마다 하나의 줄에 양의 정수 $N$이 주어진다.

출력

각 테스트 케이스마다 주어진 순서대로 한 개의 줄에,

조건을 만족하는 수열이 있다면 수열 $A_1$, $A_2$, $\cdots$, $A_N$을 공백으로 구분하여 출력한다. 조건을 만족하는 수열이 없다면 -1을 출력한다.

제한

• $1 \le T \le 5\,000$
• $2 \le N \le 10^7$
• 모든 테스트 케이스의 $N$의 합은 $10^7$을 넘지 않는다.

idea

푼건아니고 지나가다가 본 문제인데 지금 풀시간은 없고해서 잠깐 생각한 idea만 적어둠..

이런 비슷한 유형의 문제가 해밀턴 순환이 있는데

먼저 각 노드에서 합으로 제곱수가 가능한 노드를 연결해서 다음과 같은 그래프를 만든다.

예를 들어, 1노드는 3, 15, 8과 제곱수를 만들 수 있으므로 다음과 같은 그림이 그려진다.

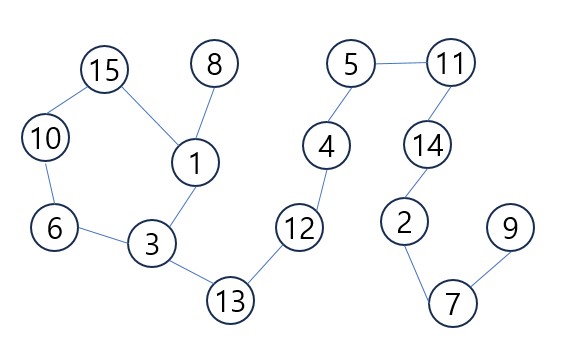
여기서 일자로 연결된(각 노드의 차원이 2인 그래프) 그래프로 만들면된다.

이때, 모든 노드의 차원을 2로 만들기 위해서는 같은 2보다 큰 차원을 가진 노드가 인접해서 존재할떄만 가능함. 노드 1과 노드 3의 차원이 3이고 이 둘사이에 인접한 edge를 끊으면 알고리즘에서 만족하는 그래프가 만들어진다.

8 - 1 - 15 - 10 - 6 - 3 - 13 - 12 - 4 - 5 - 11 - 14 - 2 - 7 - 9

즉, 그래프의 사이클이 존재하지 않으면서 모든 노드의 차원이 2이면 된다.