[논문 리뷰]A Simple Unified Framework for Detecting Out-Of-Distribution Samples and Adversarial Attack
A Simple Unified Framework for Detecting Out-of-Distribution Samples and Adversarial Attacks
[PDF] , Out-Of-Distribution, kimin Lee, Kibok Lee, Honglak Lee, Jinwoo shin
Summary
이 논문을 간단하게 요약하면, 먼저 pretrained model은 재학습하지 않고 model을 통과한 feature들을 추출한다. 이때 softmax classifier로 학습한 모델은 feature space에서 class-conditional gaussian distribution을 따르게 된다.
training sample가 모델을 통과하여 추출된 feature들을 각 class에 대한 parameter인 class-mean과 covariance를 계산한다. test sample x에 대해 mahalanobis distance를 계산하고 이를 이용한 confidence score를 사용한다. 이때 test sample x은 모든 class에 대해 confidence score를 계산하고 그 중 max값 가진 클래스 즉, test sample x에 가장 근접한 gaussian distribution에 대한 confidence score만 사용하게 된다.
그리고 이 confidence score를 통해 out-of-distribution과 in-of-distribution을 판단하는 rogistic regression 모델을 학습시켜 새로운 sample이 in/out-distribution 어디에 속하는지 판단하게 된다.
softmax classifier는 계산 특성상 confidence 비율을 나타내기 때문에 OOD Sample이 들어올 경우 모든 class에대해 고르게 confidence를 분배해야 하지만 수식 특성상(exponential) 한쪽 class에서 high-confidence로 예측되어 문제가 발생한다. 논문에서 이러한 문제점때문에 softmax와 유사한 수식을 가지는 generative classifier로 대체한다.
Fast Gradient Sign Method(FGSM)에서 아이디어를 얻어 Unseen data에 대해 일반화 성능을 높이기 위해 confidence 방향으로 Noise를 주어 In/Out distribution이 더 잘 구분 될 수 있도록 이미지를 calibration 한다. 그리고 Pretrained Network에서 high-level feature 뿐만 아니라 low-level feature를 같이 사용하여 feature 끼리 ensemble하여 모델의 성능을 높였다.
Method

먼저, 논문에서는 사전 학습된 네트워크의 feature space는 class-conditional gaussian distribution을 따를 것이라는 가정한다. 실제로 논문에서 위 그림처럼 CIFAR-10으로 학습한 resnet의 feature space는 class별로 gaussian distribution을 따르고 있다는 것을 보여주고 있습니다.
또한 Softamx classifier과 class-conditional gaussian distribution에 기반한 classifier의 수식적인 양상이 유사한데 softmax classifier의 posterior를 수식적으로 표현하면 다음과 같다.
\[P(y=c|x)=\frac{exp(\pmb{\mathbb{w}}_c^{\top} f(x) + b_c )} {\sum_{c'}{exp(\pmb{\mathbb{w}}_{c'}^{\top} f(x) + b_{c'} )}}\]여기서 $f(x)$은 마지막 layer에서 나온 feature 이고 $w_c^{\top}$와 $b_c$은 softmax classifier의 weight와 bias를 뜻한다.
다음으로 Generative classifier의 Posterior $P(y=c|x)$를 계산해야 하는데 우리가 현재 아는 정보는 feature space가 class-conditional gaussian distribution을 따른다는 것이다. 그러므로 likelihood는 다음과 같이 표현이 가능하다. 논문은 증명에서 GDA의 간단한 케이스인 LDA(Linear Discriminant Analysis)로 가정하고 진행하였다. 이때 LDA에서 모든 클래스는 같은 공분산을 가지게됨.
\[\begin{split} \mathit{Likelihood} \quad P(x|y=c)&=\mathcal{N}(x|\mu_{c},\; \Sigma) \\ &= \frac{1}{2\pi^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}} exp(-\frac{1}{2}(x-\mu_{c})^{\top}\Sigma^{-1}(x-\mu_{c})) \end{split}\]Posterior는 베이지안 룰에 의해 다음과 같은 계산식으로 표현됨.
\[\begin{split} Posterior &= \frac{Likelihood \times Prior}{Evidence} \\ P(y=c|x) &= \frac{P(x|y=c) P(y=c)}{P(x)} \\ &= \frac{P(x|y=c) P(y=c)}{\sum_{c'}{P(x|y=c') P(y=c')}} \quad (Law \; of \; total \; probabilty) \end{split}\]여기서 $Prior$는 클래스에 대한 사전 정보로 전체에서 해당 class가 차지하는 비율을 나타낸다.
\[Prior \quad P(y=c) = \frac{\beta_{c}}{\sum_{c'}{\beta_{c'}}}\]앞선 식들을 $Posterior$에 넣고 정리하면 다음과 같이 변형된다.
\[P(y=c|x) = \frac{(2\pi)^{-\frac{d}{2}} |\Sigma|^{-\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{c})^{\top}\Sigma^{-1} (x-\mu_{c})) \frac{\beta_{c}}{\sum_{c'}{\beta_{c'}}}} {\sum_{c'}{(2\pi)^{-\frac{d}{2}} |\Sigma|^{-\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{c'})^{\top}\Sigma^{-1} (x-\mu_{c'})) \frac{\beta_{c'}}{\sum_{c'}{\beta_{c'}}}}}\]여기서 공통되는 부분인 $2\pi^{-\frac{d}{2}}$, $|\Sigma|^{-\frac{1}{2}}$, $\sum_{c’}{\beta_{c’}}$을 약분하고 정리해주면 위에서 봤던 softmax classifier의 식과 매우 유사한 공식이 나온다.
\[\begin{split} P(y=c|x) &= \frac{exp(-\frac{1}{2}(x-\mu_{c})^{\top}\Sigma^{-1} (x-\mu_{c})) \beta_{c}} {\sum_{c'}{exp(-\frac{1}{2}(x-\mu_{c'})^{\top}\Sigma^{-1} (x-\mu_{c'})) \beta_{c'}}} \\ &= \frac{exp(-\frac{1}{2} \big[ x^{\top}\Sigma^{-1}x - \mu_{c}^{\top}\Sigma^{-1}x - x^{\top}\Sigma^{-1}\mu_{c} + \mu_{c}^{\top}\Sigma^{-1}\mu_{c} \big] + \ln{\beta_{c}})} {\sum_{c'}{ exp( -\frac{1}{2} \big[ x^{\top}\Sigma^{-1}x - \mu_{c'}^{\top}\Sigma^{-1}x - x^{\top}\Sigma^{-1}\mu_{c'} + \mu_{c'}^{\top}\Sigma^{-1}\mu_{c'} \big] + \ln{\beta_{c'}}) }} \\ &= \frac{exp(-\frac{1}{2}x^{\top}\Sigma^{-1}x) \cdotp exp(\mu_{c}^{\top}\Sigma^{-1}x -\frac{1}{2}\mu_{c}^{\top}\Sigma^{-1}\mu_{c} + \ln{\beta_{c}}) } {\sum_{c'}{exp(-\frac{1}{2}x^{\top}\Sigma^{-1}x) \cdotp exp(\mu_{c'}^{\top}\Sigma^{-1}x -\frac{1}{2}\mu_{c'}^{\top}\Sigma^{-1}\mu_{c'} + \ln{\beta_{c'}})}} \\ &= \frac{exp(\mu_{c}^{\top}\Sigma^{-1}x -\frac{1}{2}\mu_{c}^{\top}\Sigma^{-1}\mu_{c} + \ln{\beta_{c}}) } {\sum_{c'}{exp(\mu_{c'}^{\top}\Sigma^{-1}x -\frac{1}{2}\mu_{c'}^{\top}\Sigma^{-1}\mu_{c'} + \ln{\beta_{c'}})}} \\ &\pmb{\mathbb{w'_{c}}}^{\top} = \mu_{c}^{\top}\Sigma^{-1}, \quad b'_{c} = -\frac{1}{2}\mu_{c}^{\top}\Sigma^{-1}\mu_{c} + \ln{\beta_{c}} \\ &= \frac{ exp(\pmb{\mathbb{w'_{c}}}^{\top}x + b'_{c}) } {\sum_{c'}{ exp(\pmb{\mathbb{w'_{c'}}}^{\top}x + b'_{c'} )}} \end{split}\]이제 사전 학습된 softmax neural classifier로 부터 generative classifier를 추정하기 위해서 parameter인 class mean $\mu_{c}$와 공유 공분산 $\Sigma$을 구해야 된다. 이 parameter들은 empirical하게 training sample들로 부터 계산한다.
\[training \; samples \; \mathcal{X} = \{ (x_1,y_1), \, \cdots, (x_N,y_N) \} \\ \hat{\mu_{c}} = \frac{1}{N_c} \sum_{i:y_i=c}{f(x_i)} \, , \quad \hat{\Sigma}=\sum_{c}{\sum_{i:y_i=c}{\big[(f(x_i)-\hat{\mu_{c}})(f(x_i) - \hat{\mu_{c}})^{\top}\big]}}\]$f(\cdotp)$는 사전학습된 네트워크의 softmax classifier를 제외한 마지막 layer의 feature이고 $N_c$는 class c의 개수를 말한다.
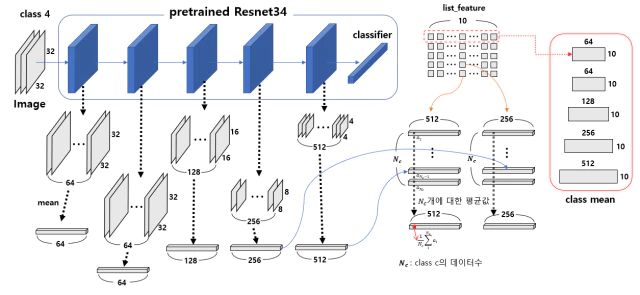
class mean을 구하는 과정은 위의 그림과 같다. 각 계층의 layer로 부터 추출된 feature를 사용하는건 feature ensemble이다. layer로 부터 추출된 feature는 channel 차원으로 평균 계산해준다. 이 vector를 class별로 따로 모아서 평균을 내준다. 이렇게 feature level 별로 생성된 class mean은 channel과 class에 대한 matrix가 생성된다.
에를들어 feature level 0(feature dim-64)에서 class 4에 대한 training sample의 vector들을 모아서 평균을 내주면 1 x 64의 vector가 되고 이 벡터는 10 x 64의 matrix에서 4행에 위치하게 된다.
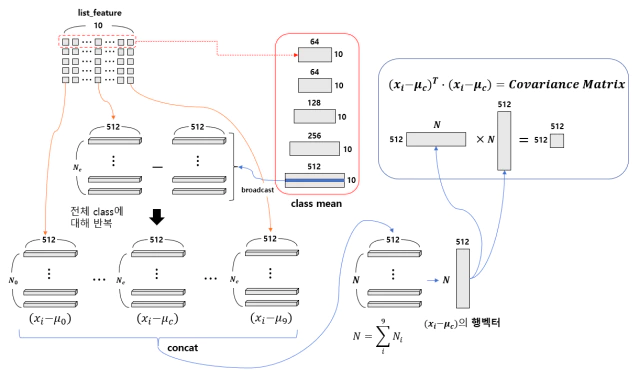
class mean을 구한 이후 공유 공분산을 구하는 과정은 위 그림에 나타냈다. 모든 sample에 대해 추출한 feature를 클래스 별로 모아 $N_c \times Dim$ matrix를 만들고 class mean에서 해당 class의 matrix을 가져와 추출한 $N_c \times Dim$ feature matrix에 빼준다. 각각의 class mean에 대해서 빼준 모든 feature들을 concat해서 $N \times Dim$의 행벡터를 만들고 행벡터를 제곱하여 Covariance matrix를 만든다.
training sample을 제외한 나머지 sample x에 대해 mahalanobis distance를 계산하여 sample x와 가장 가까운 class-conditional gaussian distribution 사이의 distance를 confidence score $M(x)$로 사용한다.
\[M(x) = \max_{c}{-(f(x)-\hat{\mu_{c}})^{\top} \Sigma^{-1} (f(x)-\hat{\mu_{c}}) }\]Mahalanobis distance 간단한 설명 펼치기/접기
- Mahalanobis distance는 어떤 sample x가 가우시안 분포의 중심으로 부터 표준 편차의 몇배 만큼 떨어져 있는 비율을 나타낸다.
- sample x를 가우시안 분포의 평균값과 표준편차로 정규화 한것과 같고 이를 1차원 가우시안 분포일때는 다음과 같다.
- 이 식은 1차 가우스 분포 함수의 지수 부분과 같다. $g(x)= \frac{1}{\sigma \sqrt{2\pi}} exp(-\frac{1}{2}(\frac{x-\mu}{\sigma})^2)$
- d차원을 가진 다변량 가우시안 분포에서의 Mahalanobis distance는 다음과 같다.
Confiden Score를 구하는 과정은 다음 그림과 같다.
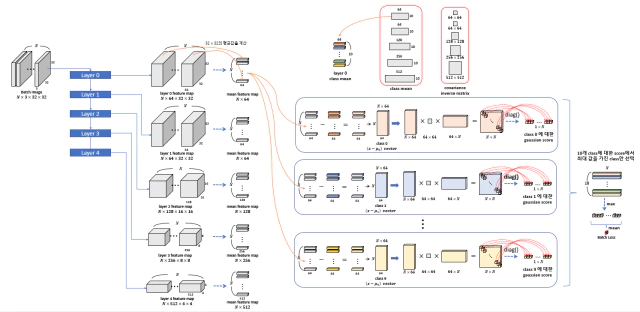
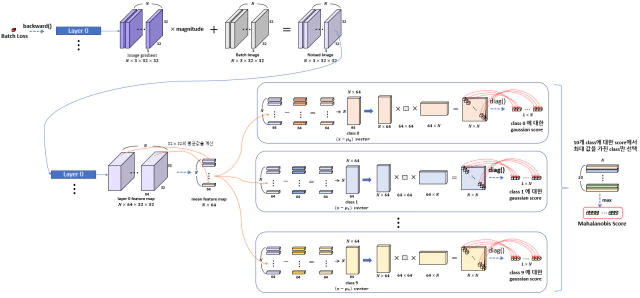
각 layer에서 추출된 feature은 같은 과정을 반복한다. 모든 class c에 대해 추출된 feature으로 confidence score를 계산하고 그 중 최대값을 사용한다. 이후 input calibration을 위해 batch에 대해 평균을 낸 값을 Loss로 사용한다.
각 샘플에 대해 $M(x)$값을 계산한 이후 classifier의 성능을 더 높이기 위해 전처리 방법을 추가하여 들어오는 이미지에 대해 calibration을 해준다. 이미지에 작은 perturbation을 추가하여 sample이 In/Out distribution이 더 잘 구분되도록 해주는 역할을 한다.
이 input calibration 방법은 Fast Gradient Sign Method(FGSM)에서 아이디어를 얻었고, FGSM은 back propagation을 통해 loss를 최소화하도록 학습하는 것을 반대로 이용하여, loss를 증가시키는 방향의 gradient를 계산하여 얻은 극소량의 pertubation을 input에 더해 줌으로써 true label에 대한 softmax score를 낮추어 mis-classification을 유도하는 방법이다.
\[FGSM \; Method \; : \; \hat{x} = x + \epsilon sign(\nabla_{x} J(\theta,x,y))\]FGSM과는 반대로 loss를 최소화하도록 하는 방향으로 pertubation을 주어 input에 대한 confidence score를 높여 주어 in-distribution sample에 대한 예측을 강화하여 더 잘 예측 되도록 도와주는 역할을 한다.
\[\begin{split} Input \; Calibratin \; : \; \hat{x} &= x + \epsilon sign(\nabla_{x}M(x)) \\ &= x - \epsilon sign(\nabla_{x} (f(x)-\hat{\mu_{\hat{c}}})^{\top} \Sigma^{-1} (f(x)-\hat{\mu_{\hat{c}}}) ) \end{split}\]여기서 $\epsilon$은 noise의 정도를 조절하고 $\hat{c}$은 sample x에서 가장 가까운 class를 나타낸다.
이제 극소량의 noise가 포함된 image가 생성되고 noised image를 다시 network에 통과시켜 아까와 같은 방법으로 confidence score를 계산한다.
이렇게 구해진 confidence score를 in-of-distribution sample에 대해 Label 0를 out-of-distribution sample에 대해 Label 1을 부여한다. 그리고 각 feature level에 구한 confidence score를 새로운 feature로 갖는 데이터로 rogistic regression model을 학습시킨다. 이렇게 학습된 model은 OOD sample일 경우 1.0에 가까운 값을 출력하고 반대로 IOD Sample일 경우 0에 가까운 값을 출력하게 된다.
Algorithm 1 Computing the Mahalanobis distance-based confidence score
Input: Test sample x, weights of logistic regression detector $\alpha_{\ell}$, noise $\varepsilon$ and parameters of Gaussian distribution ${\hat{\mu_{\ell, \, c}} \; \hat{\Sigma_{\ell}} : \forall \ell, \,c }$
Initialize Score vectors: $M(x)=[M_{\ell} : \forall \ell ]$
for each layer $\ell \in 1,…,L$ do
$\quad$Find the closest class: $\hat{c}=\underset{c}{arg min}(f(x) - \hat{\mu}_{\ell,c} )^\top \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,c})$
$\quad$Add small noise to test sample: $\hat{x}=x-\epsilon sign\big( \nabla_{x}(f_{\ell}(x) - \hat{\mu}_{\ell,\hat{c}} )^{\top} \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,\hat{c}} )\big)$
$\quad$Computing confidence score: $M_{\ell}=\max_{c} - (f_{\ell}(x) - \hat{\mu}_{\ell,c})^\top \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,c})$
end for
return Confidence score for test sample $\sum_{\ell}\alpha_{\ell}M_{\ell}$
논문에서 나타낸 전체적인 과정에 대한 알고리즘이다.
- sample에 대해 confidence score를 계산하여 closest class gaussian distribution을 찾는다.
- 가장 가까운 분포의 confidence score를 backward시켜 Input Image에 대한 gradient를 noise로 이미지에 추가한다.
- noised image를 다시 모델에 통과시켜 confidence score를 계산한다.
- 1~3과정을 모든 layer에 대해 반복한다.
- 각 layer에서 나온 confidence score를 feature로 하는 rogistic regression model을 학습시켜 In/Out 여부를 판단한다.
논문은 OOD sample 탐지 뿐만아니라 new class가 추가되는 class-incremental learning에서도 사용될 수 있다고 주장하는데 new class도 OOD class와 마찬가지로 training distribution의 범위 밖에 있기 때문에 new class를 network를 재학습 없이 분류 할 수 있다는것이 당연하다는 것이다.
논문에서는 단순히 모든 class의 공유 공분산을 업데이트하고 new class의 mean값을 계산함으로써 new class를 분류할 수 있음을 실험적으로 보여준다. 이 과정을 알고리즘으로 표현하면 다음과 같다.
Algorithm 2 Updating Mahalanobis distance-based classifier for class-incremental learning.
Input: set of samples from a new class ${x_i: \forall i = 1,…,N_{C+1}}$, mean and covariance of observed classes ${\hat{\mu}_{c}: \forall_{C} = 1,…,C}, \; \hat{\Sigma}$
Compute the new class mean: $\hat{\mu}_{C+1} \gets \frac{1}{N_{C+1}} \sum_{i} f(x_{i}) $
Compute the covariance of the new class: $ \hat{\Sigma}_{C+1} \gets \frac{1}{N_{C+1}} \sum_{i} (f(x_{i}) - \hat{\mu}_{C+1} )^{\top} $
Update the shared covariance: $ \hat{\Sigma} \gets \frac{C}{C+1} \hat{\Sigma} + \frac{1}{C+1} \hat{\Sigma}_{C+1} $
return Mean and covariance of all classes ${ \hat{\mu}_{c} : \forall_{C}=1,…,C+1, \; \hat{\Sigma} }$
먼저 OOD로 분류된(?) sample들을 new class로 가정하고 class-mean을 empirical하게 계산한다. 마찬가지로 new class를 추가하여 공유 covariance을 업데이트 해준다. 그리고 이 mean값과 공유 covariance를 통해 score를 계산한다(?) 아마도 각 layer에서 나온 feature를 통해 rogistic resgression 하는것으로 보인다(incremental learning에 대한 자세한 code는 못찾겠음).
Experiment
논문에서는 모델을 다음의 3가지 task에 대해서 성능을 평가했다.
- Out-of-distribution sample을 탐지하는 task
- FGSM[10], BIM[16], DeepFool[26], CW[3]와 같은 attack method에서 생성된 adversarial sample을 탐지하는 task
- 기존 모델에 new class가 추가되는 class-incremental learning task
Experiment 1. Detecting Out-of-Distribution samples
실험을 위해 DenseNet-100과 ResNet-34 Network로 사용했고 CIFAR-10, CIFAR-100, SVHN dataset을 training set으로 사용했다. test set으로는 TinyImageNet, LSUN을 사용했다.
학습에 사용될 dataset은 CIFAR-10, CIFAR-100, SVHN중 1개를 선택하여 In-distribution(positive) dataset으로 취급하고 나머지 training dataset은 Out-distiribution(negative)으로 취급했다. 그리고 test set은 오로지 validation에만 사용했다. 예를 들어 CIFAR-10을 training set으로 선택하면 SVHN, TinyImageNet, LSUN을 OOD dataset으로 생각하고 실험을 진행함.
평가 과정에서 test sample의 confidence score를 threshold이상 일 경우 in-distribution으로 분류하는 threshold-based detector를 사용했다.
성능지표는 true positive rate(TPR)이 95%이상인 지점에서 true negatvie rate(TNR)의 값, AUROC, area under the recision-recall(AUPR), Accuracy를 사용했다.
성능 비교를 위해 모델은 baseline method[13]과 ODIN[21]를 사용했다.
Contribution by each technique
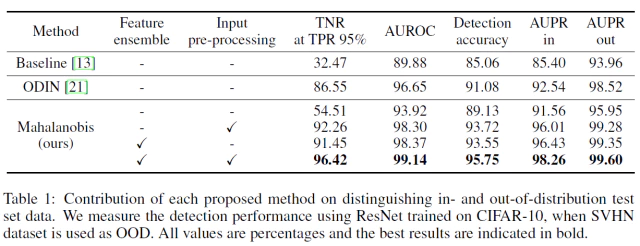
모델에 적용된 기술들이 성능 향상에 얼마나 기여 했는지를 보여주는 실험이다. baseline과 ODIN을 비교 대상으로 선택했고 모델에 Feature ensemble과 Input-preprocessing 2개의 기술을 번갈아 적용하면서 성능에 끼치는 영향을 5개의 성능지표로 평가 했다.
아무것도 적용안된 모델은 baseline method의 성능보다 좋지만 ODIN을 넘지 못했고 기술이 적용된 모델들은 모두 ODIN 성능을 넘어갔다는 점에서 Input-preprocessing과 Feature ensemble 모두 모델에 큰 영향을 미쳤다.
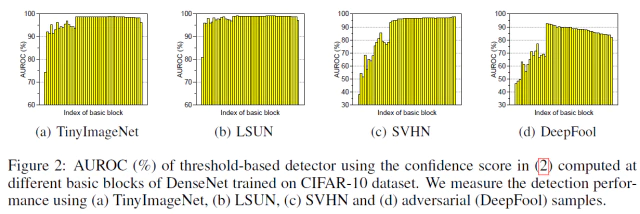
feature ensemble의 경우 DenseNet에서 basic block을 변경해 가면서 AUROC에 대한 성능을 측정했는데, low level에서 성능이 더 좋은 경우(DeepFool의 중간 layer의 경우)와 같이 low level feature에도 confidence score에 긍정적인 영향을 미치는 특성들이 있을 가능성이 높다.
하지만 그대로 low level의 의견을 반영 하기에는 반대로 악영향을 미치는 경우 성능의 편차가 커지므로 weight sum의 형태로 logistic weight 를 학습시켜 악영향을 미치는 level feature의 영향을 줄여 feature ensemble의 효과를 최대한으로 높였다.
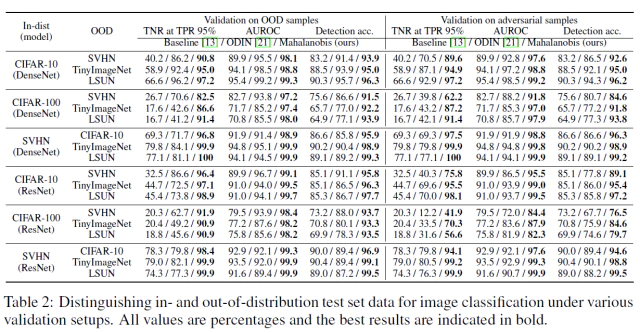
Table 2에서는 가능한 모든 데이터쌍에서 모델을 변경해가며 학습하여 baseline과 ODIN과 다양한 성능 지표에서 비교한다. 왼쪽 열인 validation on OOD samples는 logistic regression model의 decision boundary를 그릴떄 OOD sample을 포함한 경우 성능이다. 예를 들어 In-dist가 CIFAR-10이고 Out-dist SVHN인 경우 CIFAR-10에서 500개 SVHN에서 500개를 선택하여 logistic regression model을 학습했다.
반면 오른쪽열인 validation on adversarial samples는 logistic regression model의 decision boundary를 In-dist sample와 FGSM[10]으로 생성된 sample을 사용한다. 예를 들어 이 경우 In-dist는 CIFAR-10이고 Out-dist가 SVHN일때 Out-dist는 SVHN을 FGSM으로 변형한 샘플들이 들어가게 된다.
모든 dataset의 쌍의 경우에서 제안 모델의 성능이 우세해 모델이 robustness하다는 것을 보여준다. 또다른 robustness를 증명하기 위해 논문에서는 training data의 수를 매우 적게 조절해가며 성능을 측정하고 또 training set에 noisy가 섞인 경우, training sample에 현재와 전혀 다른 random label을 부여해서 학습한 모델의 성능을 측정했다.
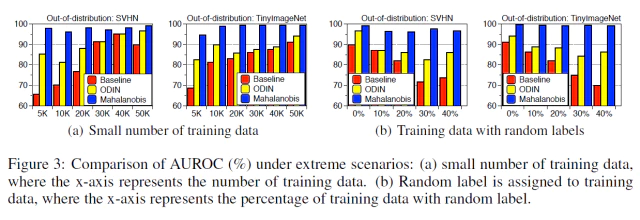
figure 3.(a)에서 training set의 수가 점점 줄어들수록 ODIN(노란색), Baseline(빨간색)의 AUROC 성능이 점점 낮아지는 경향을 보이지만 제안 모델은 성능을 유지한다.
마찬가지로 figure 3.(b)에서 Noisy label이 포함된 training set의 비율이 높아질수록 ODIN, Baseline의 성능을 낮아지지만 제안 모델의 성능은 유지되는 것을 볼 수 있다.
Experiment 2. Detecting Adversarial Attack
마찬가지로 DenseNet-100과 ResNet-34를 Network를 사용하고 CIFAR-10, CIFAR-100, SVHN dataset을 training에 사용했다. Attack method로 FGSM[10], BIM[16], DeepFool[26], CW[3]의 방법들을 사용해 training set으로 사용된 데이터의 일부를 오염시켜 사용했다.
비교를 위해 predictive uncertainty(PU)와 kernel density(KD)를 결합한 logistic regression detector와 SOTA인 Local Instrinsic Dimensionality(LID) score를 사용했다.
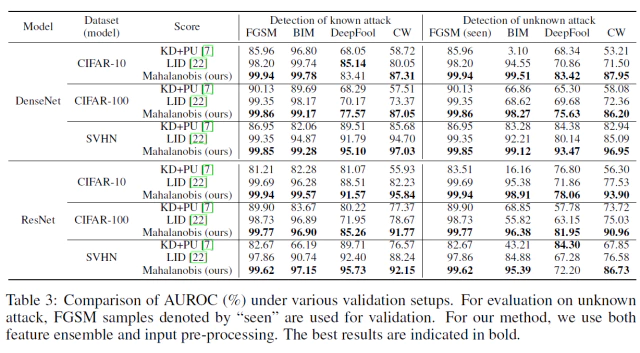
Table 3의 왼쪽 열인 Detection of Known attack은 Logistic Regression Model에 adversarial method로 부터 생성된 일부 sample을 보여준(학습)한 상태에서의 성능이다. 각 method에서 생성된 out-dist 이미지와 in-dist 이미지를 통해 logistic regression model을 fit한다.
오른쪽 열인 Detection ok unknown attack은 Logistic Regression Model에 “seen”이라고 표시된 FGSM에 대해서만 생성된 sample을 보여준 상태의 성능이다. 오른쪽 열은 simple attack method인 FGSM에서 학습된 모델이 complex attack method(BIM, DeepFool, CW) 에서도 성능이 잘나오도록 일반화가 가능한지를 보여준다.
Experiment 3. Class-Incremental Learning
class-incremental learning task 성능 실험에서 Resnet-34을 사용했고 dataset으로는 CIFAR-100과 다운샘플링된 ImageNet을 사용했다.
성능 평가를 위해 2가지의 다른 시나리오에서 테스트를 진행했다.
- 첫번째 시나리오는 CIFAR-100 class의 절반인 50개의 class를 base class로 주고 나머지 50개의 class를 new class로 취급하여 점차 추가되는 상황
- 두번째 시나리오는 CIFAR-100 class 전부를 base class로 주고 다운 샘플링된 ImageNet class중 100개의 class를 new class로 주어진 상황
모든 시나리오에서 테스트를 5번 반복한 후 5개의 평균낸 값을 최종 성능으로 평가했고 매 반복마다 랜덤하게 class가 선택되도록 했다. 성능 비교를 위해 새로운 class가 추가될때마다 fine-tuned되는 softmax classifier와 class mean을 업데이트함으로써 새로운 class에 적응하는 Euclidean classifier[25]을 선택했다.
특이 사항으로 softmax classifier의 fine-tuned하는 과정에서의 사용하는 계산과 메모리 비용을 거의 0에 근접하도록 줄이기 위해 Rebuffi & kolesnikov [29]의 방식을 선택했다.
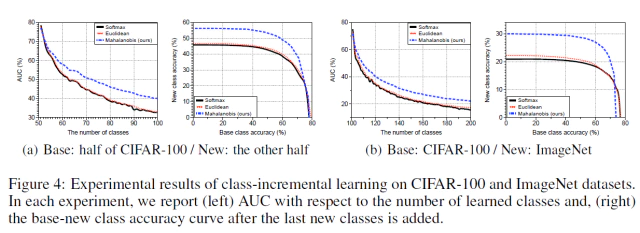
Figure 4의 왼쪽 sub-figure는 첫번째 시나리오, 오른쪽은 두번째 시나리오에 대한 성능 비교 그래프이다. sub-figure에서 왼쪽 그래프는 class가 새로이 1개씩 추가될때마다의 AUC 성능을 그래프 나타낸 것이고 오른쪽 그래프는 모든 class가 추가된 상태 마지막 상태에서의 ROC curve이다.(오른쪽 그래프는 왼쪽 AUC 성능 그래프에서 the number of classes가 100일때의 최종 상태의 roc curve 이고 class가 추가될때마다 roc curve는 새롭게 그려진다)
모든 모델이 새로운 class가 추가될때마다 AUC 성능이 떨어지지만 제안 방법 (40.0%/22.1%)과 softmax (32.7%/15.6%), Euclidean (32.9%/17.1%)로 떨어지는 정도에서 차이가 났다. 하지만 AUC가 50% 이하인 시점에서 실험 결과가 유의미(?)한지는 모르겠다.
아래는 논문 번역과 그와 관련되서 공부한 자료들을 순서없이 모은거라 참고로 보면 될거같다.
논문 번역 및 공부했던 자료 모음 펼치기
- 논문 날번역 및 의식의 흐름대로 논문을 보면서 공부했던 내용을 정리함.
Uncertainty의 유형
- Out of Distribution Test Data
- 학습할 때 한번도 보지 못한 유형의 데이터가 Test에서 사용되는 경우. 예시로 개를 학습한 모델에 대해서 고양이 사진을 주고 개의 종류를 판별하라고 하는 경우.

- Aleatoric
- 학습 데이터 자체에 노이즈가 많아서 데이터 자체에 문제가 있는 경우. 학습할 때 3가지 유형인 개,소,고양이에 대해 학습한다고 했을때 고양이 이미지가 심하게 훼손된 데이터셋으로 학습하는 경우 이후 들어오는 고양이 이미지에 대해 제대로 분류하지 못하는 불확실성 발생.

- Epistemic Uncertainty
- 주어진 데이터셋을 가장 잘 설명할 수 있는 모델을 선택할 때 생기는 불확실성. 아래 그림 처럼 어떤 모델이 해당 데이터셋에 가장 적합한지 알 수 없어서 생기는 불확실성이다. 3번째 그림이 가장 훈련 데이터에 대해 에러가 적지만 테스트 데이터에 대한 성능은 가장 낮다.
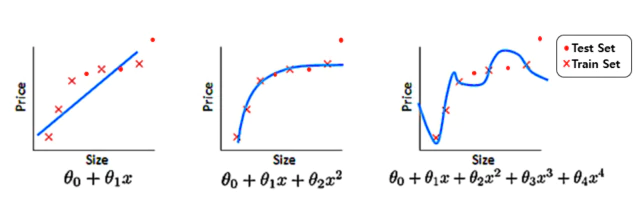
[출저] Gaussian37 블로그
논문 해석
[1]Intro
- Deep neural networks(DNNs)는 speech recognition[1], object detection, image classification과 같은 많은 분야의 classification task에서 높은 정확도를 달성했다.
- DNNs의 예측 불확실성은 적대적이거나 통계적으로 훈련 데이터의 분포로 부터 멀리 떨어진 abnormal sample을 탐지하는 문제와 매우 깊게 연관되어 있다.
- Out-of-distribution(OOD) sample을 탐지하기 위해 최근 연구들은 사후 분포(posterior distribution)[13, 21]로 부터 얻은 confidence를 이용하고 있다.
- 예를 들어 Hendrycks & Gimpel[13]는 분류기로 부터 얻은 사후 분포의 최대값을 기준 방법으로 제안하였고, 이것은 DDNs[21]의 input, output으로 처리하여 성능을 향상 시켰다.
- adversarial sample들을 탐지하기 위해, DNNs의 feature space에서 그 샘플들을 특성화 하기 위한 density estimator를 기반으로 한 confidence score를 제안하였다[7].
- 가장 최근에는 Ma et al.[22]는 Local Intrinsic Dimensionality
LID를 제안 했고 LID를 사용하여 효과적으로 test sample들의 특성을 축정할 수 있음을 실험적으로 보여주었다. - 하지만, 대부분의 이런 류의 이전 연구들은 전형적으로 OOD와 adversarial sample 둘다에 대해 평가 하지 않는다. 우리가 아는한 2개의 task에 대해 동시에 잘 동작하는 통합 detector는 없다.
- Contribution
- 이 논문에서 간단하지만 매우 효과적인 방법을 제안함. OOD와 adversarial sample을 포함한 abnormal test sample들을 탐지하는데 재학습을 필요로 하지도 않고 어떤 사전 학습된 softmax neural classifier에도 상관 없이 적용 가능함.
- 아이디어를 요약하자면 거리 기반의 generative classifier의 컨셉을 이용한 DNNs의 feature space에서 test sample의 probability density를 측정하는 것이다.
- 특히 Gaussian discriminant analysis에서 사후 분포는 softmax classifier와 거의 동일하게 보이기 때문에 class-conditional 가우시안 분포는 사전 훈련된 feature에 적합하다고 가정한다.
- 이런 가정하에 class-conditinal 분포와의 거리를 나타내는 Mahalanobis score를 사용하여 confidence score를 정의하고, 모델의 파라미터는 실힘적 경험을 바탕으로 훈련 데이터의 covariance와 class mean을 선택했다.
- 통상의 믿음과는 반대로, 해당 generative classfier를 사용하더라도 softmax classification의 정확도와 비슷한 성능을 유지하였다.
- 제안된 방법의 효율성 및 이점을 증명하기 위해 deep convolutional neural networks의 한 종류인 DensNet[14]과 ResNet[12]을 사용하여 CIFAR-10[15], SVHN[28] , ImageNet[5], LSUN[32]와 같은 다양한 데이터셋에서 이미지 분류 문제에 대해 학습시킨 모델을 사용하였다.
- 첫번째로 OOD sample들을 탐지하는 문제에서 제안 방법은 State-of-the-art(Sota) 방법인 ODIN[21]의 성능을 뛰어 넘었다.
- 특히 ODIN보다 OOD sample을 탐지하는 비율인 true negative rate(TNR)의 성능이 45.6%에서 90.9%로 상승했다.(Renset을 CIFAR-10에 대해 학습 하고 LSUN을 OOD Sample로 사용했을때)
- FGSM[10], BIM[16], DeepFool[26], CW[3]과 같이 4가지 공격 방법의 생성된 adversarial sample을 탐지에서도, 제안 방법은 Sota 측정 방법인 LID[22]의 성능을 뛰어 넘었다. CW로 부터 생성된 데이터의 TNR 성능이 82.9%에서 95.8%로 향상되었다(CIFAR-10에 대해 학습한 ResNet 모델에서 테스트).
- 제안방법은 노이즈가 포함된 훈련 데이터셋, Random Labels, 매우 적은 데이터 샘플과 같은 극한 상황에서도 hyperparameter를 선택함에 있어서 환경의 영향을 거의 받지 않아 Robust하다.
- 특히 Liang et al.[21]은 OOD sample의 validation set을 사용하여 ODIN의 hyperparameter를 조정했다. 하지만 때때로 OOD의 사전 지식을 얻지 못하는 경우에는 불가능한 방법이다.
- 제안 방법은 성능을 유지하면서 오직 training sample의 분포만을 사용하여 hyperparameter를 조정한다. 또한 FGSM과 같은 단순한 공격 방법에서 조정된 모델을 더 복잡한 공격 방법인 BIM, DeepFool, CW에서 생성된 adversarial sample을 탐지하는데 사용될 수 있음을 보여준다.
- 마지막으로 제안방법을 사전 학습된 classifier에 점진적으로 new class를 추가하는 class-incremental learning[29]에도 적용 해보았다.
- new class은 training distribution의 범위 밖에 있기 때문에(OOD sample 과 같음), new class sample을 재학습 없이 우리의 제안 방법을 사용하여 분류할 수 있는 것이 당연히 가능하다.
- 이점을 이용하여, 모든 클래스의 공유 공분산(tied covariance)을 업데이트하고 new class의 mean값을 단순히 계산함으로써 new class를 수용하는 간단한 방법을 소개한다.
- 재학습한 softmax classifier와 유클리드 거리 기반의 classifier와 같은 baseline 방법들의 성능을 뛰어 넘음.
- 이러한 실험적 증거들은 제안 방법이 few-shot learning[31], ensemble learing[19], active learning[8]과 같은 머신 러닝 문제와 관련된 곳에서 적용될 가능성을 가지고 있다고 생각한다.
[2] Mahalanobis distance-based score from generative classifier
- softmax classifier을 가진 Deep neural networks(DNNs)가 주어졌을때, Out-of-distribution(OOD)과 adversarial sample과 같은 abnormal sample을 탐지하기위한 단순하지만 효과적인 방법을 제안한다.
- 먼저, Gaussian Discriminant Analysis(GDA)으로 유도된 generative classifier를 기반으로한 confidence score에 대해 설명하고, 이 모델의 성능을 높이는 추가적인 기술에 대해서도 소개한다.
[2.1] Why Mahalanobis distance-based score?
- softmax classifier로부터 generative classifier 유도됨을 증명한다. Input $x$와 output $y$ 다음과 같다.
- 사전 학습된 softmax neural classifier의 posterior도 다음과 같다고 가정한다.
- 여기서 $\pmb{\mathbb{w}_c}$와 $b_c$는 class c에 대한 softmax classifier의 weight와 bias이고 $f(\cdotp)$은 DNNs의 끝에서 2번째 layer의 output 이다. 그런 다음 사전학습한 softmax neural classifier에 대해 어떠한 변형없이, class-conditional distribution이 다변량 가우시안 분포를 따른다고 가정하고 generaitve classifier를 얻는다.
- 공유 공분산 $\Sigma$를 가지는 $\mathit{C}$ class-conditional Gaussian distribution$\mathit{(Likelihood)}$을 다음과 같이 정의한다.
- 여기서 \(\mu_c\)는 \(c\in \{1,\cdots,\mathit{C} \}\)의 다변량 가우시안 분포의 평균 벡터이다.
- softmax classifier와 GDA사이의 이론적인 연결점을 기반으로 접근한다. 공유 공분산을 가지는 GDA기반의 generative classifier에 의해 정의된 사후 확률 분포(posterior distribution) 추정은 softmax classifier와 동일하다.
[Supplementary A] 왜 Softmax neural classifier와 class-conditional Gaussian Distribution과 동일한지?
[Supplementary A 내용 펼치기]
- 보통의 softmax classifier의 posterior는 다음과 같음.
- x가 주어졌을때 클래스에 대한 다변량 정규 분포(likelihood)는 다음과 같이 추정 가능.
- 우리는 x일때 c일 확률인 posterior를 구해야하는데 이는 bayes rule 공식 $ posterior=\frac{likelihood \times prior}{evidence} $ 으로 계산하면 되는데 이때 $evidence$는 전체 확률의 법칙으로 계산하고 $prior$는 전체에서 c의 비율을 계산하면 된다.
- 이제 $P(y=c)$와 위의 likelihood $P(x|y=c)$를 $Posterior$식에 각각 대입하고 계산한다.
-
여기서 classifier는 Linear Discriminant Analysis라고 가정하면 모든 클래스의 공분산은 같다
-
식에 포함된 상수값인 $\left| \Sigma \right|, \; \sum_{c’}{\beta_{c’}}, \; (2\pi)^{-\frac{d}{2}}$들은 분자 분모 약분 되어 사라지고 식을 전개하면 다음과 같이 된다.
- 여기서 $when \; B \; is \; symmetric \;matrix, \; A \cdotp B \cdotp C = C \cdotp B \cdotp A $을 이용하여 $ x^{\top} \Sigma^{-1} \mu_{c} = \mu_{c}^{\top} \Sigma^{-1} x$ 이므로 식에 대입하면 다음과 같이 정리된다.
- 위 식에서 공통된 부분인 $ exp(-\frac{1}{2}(x^{\top} \Sigma^{-1} x) )$ 을 따로 빼내어 다음과 같이 약분할 수 있다.
- 위 식에서 $\pmb{\mathbb{w}}_{c} = \mu_{c}^{\top} \Sigma^{-1} , \; b_c=\frac{1}{2}\mu_{c}^{\top} \Sigma^{-1} \mu_{c} + \ln{\beta_{c}}$ 이라하고 치환하면 다음과 같이 softmax classifier의 형태가 된다.
-
그러므로 사전 학습된 softmax classifier $f(x)$의 feature도 역시 class-conditional Gaussian distribution을 따른다고 할 수 있다.
-
사전 학습된 softmax neural classifier로 부터 generative classifier의 parameter를 추정하기 위해서, 실험적으로 training samples $\{(x_1,y_1), \, \cdots, \, (x_N,y_N)\} $의 공분산과 class mean을 다음과 같이 계산한다.
- 여기서 $\mathit{N}_c$ 는 class label c를 가지는 training sample의 수이다. 이것은 MLE(최대 우도 추정)에서 training sample에 대해 공유 공분산을 가지는 class-conditional Gaussian distribution에 fitting하는 것과 동일하다.
Mahalanobis distance-based confidence score
- 위에서 유도된 class-conditional Gaussian distribution을 사용하여 sample x와 가장 가까운 class-conditional distribution 사이의 Mahalanobis distance를 사용한 confidence score $M(x)$를 다음과 같이 정의 한다.
Mahalanobis distance 간단한 설명 펼치기
- Mahalanobis distance는 어떤 sample x가 분포의 평균값으로 부터 표준 편차의 몇배 만큼 떨어져 있는 비율을 나타낸다. 1-d gaussian distribution 일때는 다음과 같다
-
이 식은 1차 가우스 분포 함수의 자연 상수의 지수 부분과 같다. $g(x) = \frac{1}{\sigma\sqrt{2\pi}} exp(-\frac{1}{2} \big( \frac{x-\mu}{\sigma} \big)^2 )$
-
이를 일반화한 다변량 가우스 분포 함수의 지수 부분으로 나타내면 Mahalanobis distance가 된다.
-
이 metric은 test sample의 probabilty의 log값을 측정하는 것과 같다. 여기서 주목해야할 부분은 abnormal sample들은 이상치를 탐지하기 위한 이전 연구들[13, 21]에서 사용된 softmax-based posterior distribution의 “label-overfitted”된 output space보다 DNNs의 representation space에서 더 잘 특징화(characterize)할 수 있다는 것이다.
-
softmax classifier는 softmax decision boundary로 부터 멀리 떨어져 있는 abnormal sample에 대해서도 심지어 높은 confidence를 가지는 posterior distribution으로 confidence score를 얻었기 때문이다.
-
이러한 단점을 보안 하기 위해 Softmax classifier를 사용하지 않고 DNN feature를 사용하여 adversarial sample을 탐지하는 Feinman et al.[7] 과 Ma et al.[22]의 연구가 있지만 이러한 연구들은 Mahalanobis distance를 사용하지 않고 단순히 Euclidean distance를 사용하였음.
-
Experimental supports for generative classifiers
- 학습된 DNN의 feature가 Gaussian Distriminant Analysis(GDA) estimation에 도움이 된다는 가설을 평가하기 위해 다음과 같은 식으로 classification accuracy를 측정함.
-
이 식은 uniform class prior를 가진 generative classifier의 posterior distribution을 사용하여 class label을 예측한다는 뜻이다.
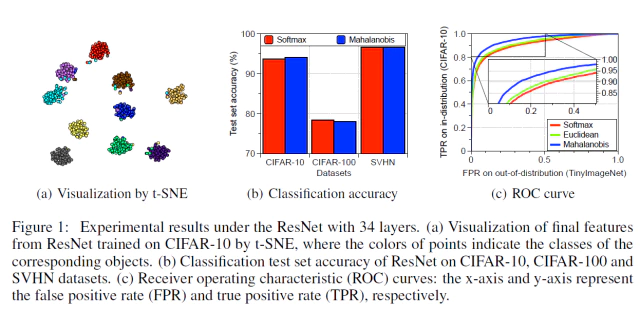
- 흥미롭게도 scratch로 학습한 generative classifier의 성능이 softmax와 같은 discriminative classifier보다 성능이 떨어질것이라는 일반적인 통념과는 다르게 Figure 1(b)를 보면 Mahalanobis distance classifier의 성능(blue bar)이 거의 softmax classifier의 성능(red bar)와 비슷한 것을 볼 수 있다.
-
Figure 1(a)는 CIFAR-10 test sample들을 DNN에 통와시켰을 때 마지막 layer의 feature를 t-SNE[23]으로 임배딩한 것을 보여준다.(점의 색깔은 Object의 class를 나타냄)
- embedding space에서 10개의 모든 class가 깔끔하게 분리된 것을 볼 수 있음.
-
추가로, Out-of-distribution sample을 탐지하는데 Mahalanobis distance-based metric이 매우 유용하게 사용될 수 있음을 보여 준다.
-
성능 평가를 위해 test sample x에 대해 Confidence score $M(x)$의 값을 계산하고 그 값이 어떤 threshold 이상이면 positive로 판단하는 단순한 detector 를 사용하여 ROC curve를 그림.
- 데이터로부터 계산된 class mean만을 이용한 Euclidean distance를 비교로 사용했다. Figure 1(c)를 보면 Mahalanobis distance 기반 방법(blue)이 Euclidean 기반 방법(green)과 maximum of the softmax distribution(red)보다 ROC 성능이 높은 것을 볼 수 있다.
[2.2] Calibration techniques
Input pre-processing
- In-of-distribution sample과 Out-of-distribution sample을 더 구분이 잘되게 만들기 위해서, test sample에 제한된 작은 noise를 추가하였다. 각각의 test sample $x$에 대해 다음과 같은 small perturbation을 추가하여 전처리된 sample $\hat{x}$를 계산했다.
-
위 식에서 $\varepsilon$은 noise의 정도를 조절하고 $\hat{c}$는 가장 가까운 class를 나타낸다.
-
adversarial attacks[10]와는 다르게 제안된 confidence score가 증가할수록 noise는 생성된다.
- Fast Gradient Sign Method(FGSM) 방식에서 아이디어를 얻었으며, Back propagation을 통해 loss를 최소화하도록 학습하는 것을 반대로 이용하여, loss를 증가시키는 방향의 gradient를 계산하여 얻은 극소량의 pertubation을 input에 더해 줌으로써 true label에 대한 softmax score를 낮추어 mis-classification을 유도함
- FGSM과는 반대로 이 논문에서는 pertubation을 gradient방향으로 빼줌으로써 주어진 input에 대한 confidence score를 높여주는 방향으로 in-distribution sample에 대한 예측을 강화하여 out-of-distribution sample과 더 잘 분리될 수 있도록 도와 주는 역할을 함.
[출저] hoya12 블로그
- 이와 비슷한 방법으로 [21]에서 predict label의 softmax score를 사용한 Noise를 추가함.
Feature Ensemble
-
성능을 더 높이기 위해 confidence score를 계산하는데 final feature 뿐만아니라 DNNs의 low-lebel feature들도 추가하는 것을 고려함.
-
training data가 주어지면 $\ell$-th hidden feature를 $f_{\ell}(x)$으로 표시하고 그때 들어오는 입력 x에 대하여 class mean과 tied covariance를 각각 \(\hat{\mu}_{\ell,c} \,\), \(\; \hat{\Sigma}_{\ell}\)이라고 표시한다.
-
각각의 test sample x에 대해서 다음의 공식으로 $\ell$-th layer의 confidence score를 계산한다.
- low-feature로 부터 더 많은 상세한 정보를 추출함으로써 confidence score를 더 잘 조정할 수 있는 score를 얻을 수 있다.
- 각 layer에 대해 confidence score를 구하는 알고리즘은 다음과 같다.
Algorithm 1 Computing the Mahalanobis distance-based confidence score
Input: Test sample x, weights of logistic regression detector $\alpha_{\ell}$, noise $\varepsilon$ and parameters of Gaussian distribution ${\hat{\mu_{\ell, \, c}} \; \hat{\Sigma_{\ell}} : \forall \ell, \,c }$
Initialize Score vectors: $M(x)=[M_{\ell} : \forall \ell ]$
for each layer $\ell \in 1,…,L$ do
$\quad$Find the closest class: $\hat{c}=\underset{c}{arg min}(f(x) - \hat{\mu}_{\ell,c} )^\top \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,c})$
$\quad$Add small noise to test sample: $\hat{x}=x-\epsilon sign\big( \nabla_{x}(f_{\ell}(x) - \hat{\mu}_{\ell,\hat{c}} )^{\top} \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,\hat{c}} )\big)$
$\quad$Computing confidence score: $M_{\ell}=\max_{c} - (f_{\ell}(x) - \hat{\mu}_{\ell,c})^\top \hat{\Sigma}_{\ell}^{-1} (f_{\ell}(x) - \hat{\mu}_{\ell,c})$
end for
return Confidence score for test sample $\sum_{\ell}\alpha_{\ell}M_{\ell}$

-
Figure 2는 CIFAR-10 dataset에 대해 학습한 DenseNet의 basic block을 변경하면서 confidence score를 계산한 ROC curve이다. SVHN[28], LSUN[32], TinyImageNet과 같은 OOD sample과 DeepFool[26]에 의해 생성된 adversarial sample에 대한 성능을 보여준다. LSUN, TinyImageNet, DeepFool에서는 final feature와 비교하여 때때로 low-level feature의 성능이 더 나은 경우가 있다. 그래서 성능 향상을 위해 Algorithm 1처럼 모든 layer의 feature를 사용하여 confidence score를 계산하고 각 layer의 score는 weight sum을 통하여 전체적인 confidence score를 계산한다.
-
validation sample을 사용한 logistic regression detector를 training하면서 각 layer의 weight ratio $\alpha_{\ell}$을 선택한다. 이러한 score weighted averaging은 몇개의 layer로부터 얻은 score가 유효하지 않을 경우 거의 0에 근접한 weight를 주어 전체적인 성능 하락을 방지 한다.
[2.3] Class-Incremental learning using Mahalanobis distance-based score
- 더나아가 Mahalanobis distance-based score를 class-incremental learning task[29]에서도 사용될 수 있다.
- class-incremental learning은 base class에 대해 사전 학습한 classifier를 new class가 생길때 마다 점진적으로 업데이트하여 new class를 수용함.
- 이 task는 제한된 메모리로 catastrophic forgetting[24]를 해결해야하기 때문에 매우 어렵다. 이를 해결하기 위해 최근 연구들은 모델 생성과 데이터 샘플링에 관련된 새로운 학습 방법을 개발하는 방향으로 진행되고 있지만 이러한 학습 방법은 비싼 학습 비용을 발생시킨다.
- 그래서 제안된 confidence score를 기반으로 복잡한 훈련방법을 사용하지 않는 단순한 classification 방법을 개발했다.
- 이 방법을 사용하기 위해서는 첫번째 가정으로 기본 class에 대해 충분히 잘 사전 학습된 모델이 있어야하는데 인터넷상에 큰 데이터세트로 학습된 Resnet과 같은 모델등이 많기 때문에 적용에 큰 어려움은 없다.
- 잘 사전학습된 모델을 사용하는 경우 OOD sample을 잘 탐지할 뿐만아니라 base class로 학습한 represetation이 new class를 잘 특징화 할 수 있으므로 new class를 잘 구별할 수 있다.
- 이러한 점을 기반으로 다음의 공식을 기반으로 class mean과 covariance를 단순히 계산하고 업데이트하므로써 new class를 수용하는 Mahalanobis distance-based classifier를 Algorithm 2에서 설명한다.
Algorithm 2 Updating Mahalanobis distance-based classifier for class-incremental learning.
Input: set of samples from a new class ${x_i: \forall i = 1,…,N_{C+1}}$, mean and covariance of observed classes ${\hat{\mu}_{c}: \forall_{C} = 1,…,C}, \; \hat{\Sigma}$
Compute the new class mean: $\hat{\mu}_{C+1} \gets \frac{1}{N_{C+1}} \sum_{i} f(x_{i}) $
Compute the covariance of the new class: $ \hat{\Sigma}_{C+1} \gets \frac{1}{N_{C+1}} \sum_{i} (f(x_{i}) - \hat{\mu}_{C+1} )^{\top} $
Update the shared covariance: $ \hat{\Sigma} \gets \frac{C}{C+1} \hat{\Sigma} + \frac{1}{C+1} \hat{\Sigma}_{C+1} $
return Mean and covariance of all classes ${ \hat{\mu}_{c} : \forall_{C}=1,…,C+1, \; \hat{\Sigma} }$
[3] Experimental results
- 이 섹션에서는 다양한 vision dataset CIFAR-10[15] SVHN[28], ImageNet[5], LSUN[32]에서 ReNet[12], DenseNet[14]과 같은 deep nueral network를 사용하여 제안된 방법이 얼마나 효과적인지를 입증할 것이다.
- 공간의 부족함으로 인해 더욱 자세한 실험 세팅과 결과는 보충 자료에서 설명할 것이다.
- 우리의 코드는 https://github.com/pokaxpoka/deep_Mahalanobis_detector에서 이용가능하다.
[3.1] Detecting out-of-distribution samples
[3.1.1] Setup
- out-of-distribution(OOD) sample을 찾는 문제를 위해, DenseNet(100 Layers)과 ResNet(34 Layers)을 CIFAR-10, CIFAR-100, SVHN dataset을 분류하기 위해 학습했다.
- 학습에서 사용된 dataset은 in-distribution(positive) dataset으로 간주하고 나머지는 OOD(negative) dataset으로 취급했다.
- test dataset은 학습 과정에는 관여하지 않고 오직 평가를 위해 사용되었다.
- 게다가 TinyImageNet(ImageNet dataset의 일부)과 LSUN dataset은 OOD로 취급되어 테스트되었다.
- 평가 과정에서 우리는 test sample의 confidence score를 측정하는 threshold-based detector를 사용하고, 이 confidence score가 threshold이상 일 경우 test sample은 in-distribution으로 분류하였다.
-
다음과 같은 방법으로 성능을 측정하였다. true positive rate(TPR)이 95%이상인 지점에서의 true negative rate(TNR), area under hte receiver operating characteristic curve(AUROC), the area under the precision-recall curve(AUPR), accuracy
-
비교를 위해 maximum value of the posterior distribution에서 정의된 confidence score을 사용하는 baseline method[13]과 the state-of-the-art인 ODIN[21], ODIN은 maximum value of the processed posterior distribution에서 confidence score를 정의했다.
- 제안 방법에서, DenseNet(or ResNet)의 dense(or residual) block의 끝마다 confidence score를 추출했다.
- 각 conv layer에서 추출된 feature map은 계산적인 효율을 위해 average pooling에 의해 차원 감소를 했다: $\mathcal{F} \times \mathcal{H} \times \mathcal{W} \rightarrow \mathcal{F} \times 1$, 여기서 $\mathcal{F}$는 channel의 개수를 의미하고 $\mathcal{H} \times \mathcal{W}$은 feature map의 크기를 의미한다.
- Algorithm 1에서 보여줬듯이 logistic regression detector의 output을 최종 confidence score로서 사용한다.
- 모든 hyperparameter들은 분리된 validation set에서 선택된다.
- 분리된 validation set은 in과 out에서 각각 선택된 1,000개의 이미지로 구성된다.
- Ma et al[22]과 유사하게 logistic regression detector의 weight들은 nested cross validation을 사용하여 학습된다.
- class label은 in-distribution에 대해 positive를 할당하고 OOD sample에 대해서는 negative를 할당한다.
- 실제로는 OOD validation dataset은 존재하지 않기 때문에, in-distribution(positive) sample과 FGSM[10]에 의해 생성된 adversarial(negative)에 해당하는 sample들을 사용하여 hyperparameter를 튜닝하는 것을 고려했다.
[3.1.2] Contribution by each technique and comparison with ODIN

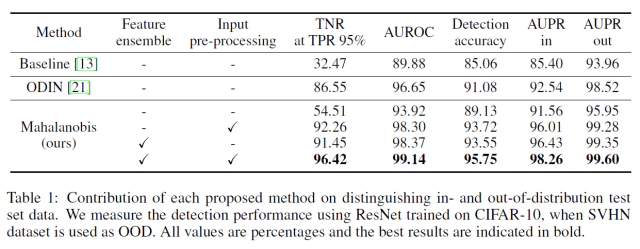
- Table 1에서 ODIN과 baseline method를 비교로 우리 제안 했던 기술들(feature ensemble, input calibration)들의 성능에 대한 기여를 보여준다.
- CIFAR-10으로 학습된 ResNet을 SVHN을 OOD sample로 사용한 탐지 성능을 측정했다.
- 여기서 추가 기술들을 점진적으로 적용했을때 성능도 같이 점진적으로 향상되는것을 보여준다.
- 제안 방법은 input calibration과 feature ensemble없이도 baseline method의 성능을 넘어선다.
- 이것은 제안 방법이 posterior distribution과 비교하여 OOD sample을 매우 효과적으로 특성화(characterize)할 수 있다는 것을 암시한다
- feature ensemble과 input calibartion을 사용하여 탐지 성능을 ODIN과 비교할만할 정도로 향상 시켰다.

- Table 2에서 왼쪽 열인 Validation on OOD samples에서 모든 dataset 쌍에서 ODIN과 탐지 성능을 비교했다.
- 모든 테스트 케이스에서 제안 방법은 ODIN과 baseline method의 성능 보다 높았다.
- 특히 제안 방법은 TNR의 성능에서 두드러졌는데 CIFAR-100으로 학습된 DensNet에서 LSUN sample을 탐지한 비율이 ODIN과 비교하여 41.2%에서 91.4%로 향상되었다.
[3.1.3] Comparison of robustness
- 제안 방법의 robustness를 평가하기 위해, 모든 hyperparameter는 FGSM[10]으로 생성된 adversarial sample과 in-distribution만 사용하여 조정(tuning)했다.
- Table 2의 오른쪽 열에서 볼 수 있듯이, ODIN의 성능은 몇몇 케이스(SVHN에서 학습한 DenseNet)에서 baseline method보다 성능이 떨어졌지만, 제안 방법은 여전히 모든 케이스에서 ODIN과 baseline method의 성능을 뛰어넘었다.
- OOD없이 학습된 제안방법은 OOD을 포함하여 학습된 ODIN의 성능보다 높았다.
- 제안방법의 robustness를 다양한 training setup에서 성능을 증명했다.
- 제안방법은 training sample의 class mean과 covariance를 경험적 기반으로 사용하기 때문에 training data 특성에 영향을 받을 수 있다는 단점이 있다.
- robustness를 증명하기 위해 CIFAR-10 dataset에서 random label로 할당되고 training data의 수를 다양하게 조절해서 ResNet을 학습한 모델의 탐지 성능을 측정했다.
- Figure 3에서 볼 수 있듯이 제안 방법(blue bar) noisy data을 포함하거나 적은 수의 training sample에서 심지어 높은 탐지 성능을 유지 했지만 ODIN(yellow bar), basline(red bar)는 성능을 유지하지 못했다.

- 마지막으로, 표준적인 cross entropy loss로 학습된 softmax neural classifier을 사용한 제안 방법의 성능은 confidence loss[20]으로 학습된
softmax neural classifier을 사용한 ODIN의 성능보다 높았다.
- confidence loss[20]은 posterior distribution을 calibrate하기 위해 generator와 classifier를 결합하여 학습한다. 심지어 이러한 모델을 학습하는 것의 연산 비용이 비싸다.
[3.2] Detecting adversarial samples
[3.2.1] Setup
- adversarial sample을 탐지하는 문제를 위해 DenseNet과 ResNet을 CIFAR-10, CIFAR-100, SVHN dataset을 분류하는 것에 대해 학습하고 성능 측정을 위해 이 dataset들을 positive sample로 사용했다.
- 다음의 attack method: FGSM[10], BIM[16], DeepFool[26], CW[3]들로 생성된 adversarial image를 negative sample로 사용했다. 이 attack method에 대한 상세한 설명은 보충 자료에서 찾아 볼 수 있다.
- 비교를 위해 predictive uncertainty(PU)와 kernel density(KD)를 결한한 logistic regression detector를 사용했다.
- 또한 비교를 위해 SOTA인 local intrinsic dimensionality(LID) score를 사용했다.
- 다음의 [7, 22]에서 비슷한 전략을 사용한다. original test sample의 10%을 랜덤으로 선택하여 logistic regression detector를 학습 하는데 사용하고 나머지 test sample을 평가에 사용한다.
- nested cross-validation을 training set에서 사용하여 모든 hyperparameter를 조정한다.
[3.2.2] Comparison with LID and generalization analysis

- Table 3의 왼쪽 열은 모든 normal과 adversarial 쌍에 대한 logistic regression detector의 AUROC score를 표시했다. 대부분의 케이스에서 제안 방법의 성능이 제일 뛰어났다.
- 특히 CIFAR-10으로 학습된 ResNet을 사용하여 CW Sample을 찾을 때 성능이 LID의 82.2%에서 제안방법의 95.8%으로 성능이 높아졌다.
- [22]와 유사하게 제안 방법이 simple attack으로 조정되어서 일반화 되어 더욱 complex attack을 탐지할 수 있는지 아닌지를 평가했다.
- 마지막으로 FGSM에 의해 생성된 sample을 사용하여 logistic regression detector를 학습했을때의 탐지 성능을 측정했다.
- Table 3의 오른쪽 열에서 표시한 것처럼 FGSM에서 학습한 제안방법이 BIM, DeepFool, CW과 같은 더욱 복잡한 공격에 대해서도 정확하게 탐지하는 것을 볼 수 있다.
- 비록 LID가 일반화 성능이 좋지만 제안 방법은 여전히 모든 케이스에서 성능이 높았다.
- 실험 결과를 보면 자연스럽게 LID가 OOD Sample을 탐지하는데 유용한지 아닌지 질문이 떠오른다.
- 정말로 모든 테스트 케이스에서 제안방법이 LID의 성능과 비교하여 높은지 아닌지를 보충자료에서 비교했다.
[3.3] Class-incremental learning
[3.3.1] Setup
- class-incremental learning task를 위해 ResNet-34을 CIFAR-100과 다운샘플링된 ImageNet[4]에 대해 분류하도록 학습했다.
- Section 2.3에 설명한것 처럼, 우리는 충분한 양의 기본 class들로 사전 학습된 classifier과 새로운 class에 해당하는 dataset이 점진적으로 하나씩 하나씩 주어지는 것으로 가정했다.
- 특별히, 2가지의 다른 시나리오에서 테스트 했다.
- 첫번째 시나리오는 CIFAR-100 class의 절반을 기본 클래스로 주어지고 나머지를 new class로 주어진 상황
- 두번째 시나리오는 CIFAR-100의 모든 class가 기본 클래스로 주어지고 다운 샘플링된 ImageNet의 class중 100개를 new class로 주어진 상황
- 모든 시나리오에서 테스트를 5번 반복한 이후 평균낸 값을 최종 성능으로 사용하고 매 반복마다 랜덤하게 class 나누었다.
- 새로운 class가 들어올때마다 fine-tuend되는 softmax classifier와 오직 class mean을 계산함으로써 새로운 class에 적응하는 Ecludean classifier[25]를 성능 비교 대상으로 고려했다.
- softmax classifier에서 거의 0에 근접하는 cost training[25]을 달성하기 위해 softmax layer만 업데이트하고 Rebuffi & Kolesnikov [29]의 memory management을 따랐다. 이 memory management는 제한된 메모리에 old class들의 일부 작은 샘플들을 저장하는 것이다. 여기서 이 제한된 메모리의 크기는 mahalanobis distance-based classifier의 parameter들을 저장하는 메모리의 크기와 비슷하다.
- 다시말해, softmax classifier의 학습을 위해 유지되는 old exemplars의 수는 학습된 class의 수와 hidden feature의 차원(실험에서는 512차원)의 합으로 선택 됩니다.
- 평가에서 [18] 먼저 new class 점수에 대한 추가 편향을 조정하여 base-new 정확도 곡선을 그리고, base-new 클래스 정확도를 평균화하면 base class와 new class 간의 성능 측정이 불균형해질 수 있으므로 곡선 아래 면적(AUC)을 측정합니다.

[3.3.2] Comparison with other classifiers
- Figure 4은 위에서 언급된 2가지 시나리오에서 방법들의 incremental learning 성능을 AUC로 비교했다.
- 각각의 sub-figure는 학습된 class의 수에 대응되는 AUC에 대한 그래프(left)과 마지막 new class가 추가된 후 그려진 base-new class 정확도 그래프(right)이다.
- 제안된 Mahalanobis distance-based classifier는 비록 오른쪽 figure 4(b)에서는 작은 차이(catastrophic forgetting issue 때문)가 났지만 new class의 수가 증가할수록 큰폭으로 성능 차이가 났다.
- 특히, 제안 방법은 첫번째(두번쨰) 시나리오 실험에서 new class가 모드 추가된후의 성능이 40.0% (22.1%)로 softmax classifer의 성능인 32.7% (15.6%)와 Euclidean distance classifier의 성능 32.9% (17.1%) 보다 더 성능이 더 높았다.
- 또한 CIFAR-100을 base class로 두고 CIFAR-10을 new class로 지정하고 전반적인 실험 과정이 유사한 실험 결과를 보충 자료에 표시했다.
- 추가적인 실험 결과는 제안방법의 confidence score가 다른 것과 비교하여 더 성능이 좋다는 것을 증명했다.
[4] Conclusion
- 단순하지만 OOD와 adversarial에 대한 abnormal test sample을 잘탐지하는 효과적인 방법을 제안.
- 본질적으로, main idea는 LDA 추정 기반의 generative classifier로 부터 나왔으며 새로운 confidence score도 이것을 기반으로 함.
- feature ensemble과 input preprocessing과 같은 calibration technique을 통해 많은 task에 대해 robust한 성능을 가지게함.
- OOD sample, adversarial attack, class incremental learning
- 이 방법은 training data가 noisy, ranodm label, data sample의 개수가 매우 적은 극한 상황에서도 hyper parameter의 설정이 매우 자유로워 robust하다.
선형 판별 분석(Linear Discriminant Analysis)
[참고] ratgo’s blog
- LDA(Linear Discriminant Analysis)는 특정한 축(axis)에 사영(projection)한 이후 범주(category) 혹은 클래스를 잘 구분하는 직선인 Decision Boundary를 찾는 것이 목표.
- 2개의 클래스를 잘 구분하기 위해선 클래스들이 사영된 축에서 클래스 사이의 중심(평균)이 서로 멀고 각 클래스의 분산이 작아야 된다.
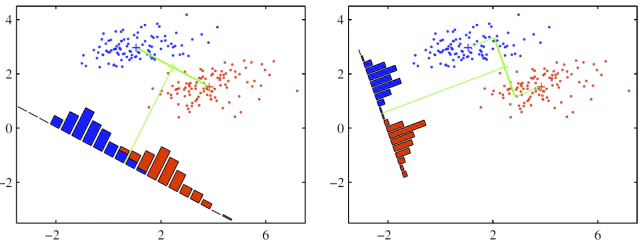
1. LDA에 대한 첫번째 접근
- $p$차원의 입력 $vector \; x$가 $\mathbf{w}$라는 축에 사영된다고 할때 축 위에서 사영된 1차원의 스칼라 값을 $y$라고 하고 두 클래스 $C_{1}$과 $C_{2}$ 각각에 대해 $N_{1}$, $N_{2}$개의 데이터가 있다고 하자.
- 먼저 사영후 두 클래스의 중심인 평균이 서로 멀어야 된다. 이때 $m_1$과 $m_2$를 축에 사영하여 $m_{1}’$과 $m_{2}’$를 만들고 그 사이의 거리 $\overline{m_{1}’ m_{2}’}$가 최대가 되는 축 $\mathbf{w}$를 찾으면 된다.
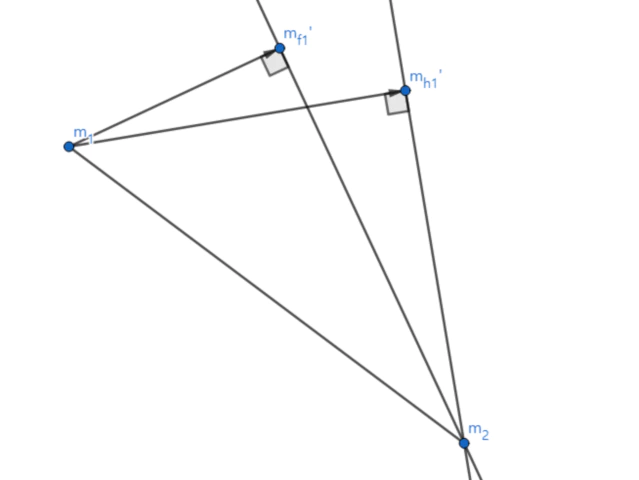
- 여기서 축 $\mathbf{w}$에 사영된 $\overline{m_{1}’ m_{2}’}$의 길이는 다음과 같다.
- 다음으로 사영후 두 클래스 각각의 분산이 작아야 된다. 클래스가 넓은 범위에 걸쳐 사영되면 범위가 겹치는 곳이 많아지므로 클래스를 구분하기 어려워지므로 좁은 범위에 사영되게 하기 위해 분산을 작게한다. k class의 사영된 값을 $y_{k}$, 평균 $m_{k}$, 분산을 $s_{k}^{2}$ 라고 한다. 이때 분산은 다음과 같이 계산된다.
- 이제 축에 사영된 중심의 거리는 최대화 하고 분산은 최소화해야 된다. 다음과 같은 함수를 만들고 이를 최대화 하면 된다.(식을 단순화 하기 위해서 두 개의 클래스만 가정)
- 여기서 $J(\mathbf{w})$ 함수를 최대화하는 $\mathbf{w}$를 찾아야 하므로$\mathbf{w}$에 대한 함수로 만들기 위해 위의 식들을 대입하여 정리하면 다음과 같다.
- 여기서 식을 간단하게 하기 위해 식을 치환한다.
- 이제 $J(w)$의 최대값을 구하기 위해 미분을 하여 $J^{\prime}(w)=0$인 $w$값을 찾으면 된다.
- 행렬 미분을 이용하여 정리하면 다음과 같다.
- 여기서 $J^{\prime}(w)=0$을 만족하는 w로 고정 되어 있으므로 $J(w)$은 스칼라 값이다. 그래서 식을 다음과 같이 변형하면 고유값 형태의 문제가 된다.
- 즉 두개 클래스의 $vector \; x$들을 $\mathbf{w}$축에 사영했을때 서로의 중심 거리가 최대가 되고 각 클래스의 분산이 최소가 되는 $\mathbf{w}$는 $(S_{W}^{-1} S_{B})$의 고유 vector이다.
2. LDA에 대한 두번째 접근(Bayes rule)
- 클래스 $w_{1}$, $w_{2}$가 있고 데이터 x가 있다고 할때 목표인 판별 함수(discriminant function) $p(w_{1}|x)$와 $p(w_{2}|x)$ 즉, Posterior를 구해야한다. 하지만 이는 실제로 매우 구하기 힘드므로 베이즈 정리를 사용하여 Likelihood와 Prior로 구해야된다. 베이즈 정리에 의해 Posterior는 다음과 같다.
- 여기선 두개의 클래스로 가정했으므로 전체 확률의 법칙을 적용하면 다음과 같은 식이 된다.
-
거의 대부분의 실제 데이터는 가우스 정규 분포(Gaussian normal distribution)를 따른다. 현재 우리가 판별하고자 하는 데이터 x도 다변량 정규 분포(Multivariate Gaussian Normal distribution)를 따른다고 가정한다. 따라서 $w$에대한 $x$의 확률인 likelihood 즉, $p(x|w)$는 다변량 정규 분포 확률 밀도 함수가 된다.
-
이때 다변량 정규 분포의 차원은 d이고 이때 평균 $\mu$과 공분산 $\Sigma$는 다음과 같다.
- x일때 어떤 클래스인지 판별하는 함수를 판별 함수(discrimiant function)이라고 한다. 여기서 posterior를 판별 함수로 사용하고 posterior의 계산을 쉽게 하기 위해 log-posterior를 사용한다. 판별 함수는 클래스의 확률이 높게 나오면 해당 클래스로 분류하기 때문에 단조 함수인 log를 사용해도 성질이 변하지 않는다.
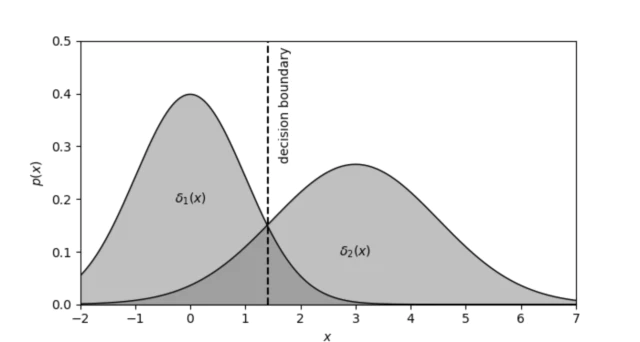
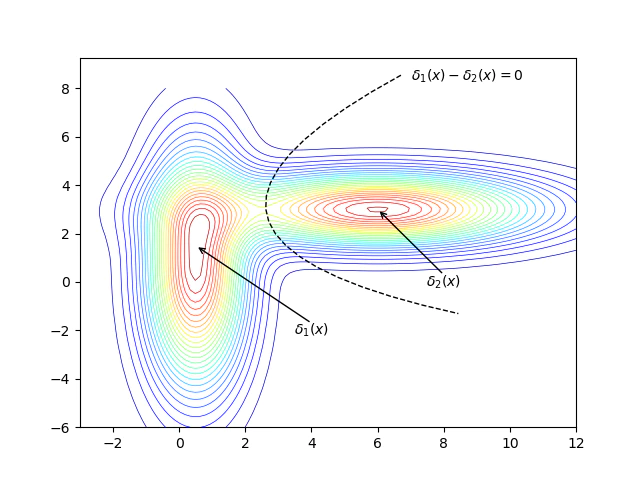
- 이제 두 클래스를 판별하는 결정 경계(Decision Boundary)를 정해야 하는데 결정 경계는 위 그림처럼 보통 두 판별 함수의 값이 같은 곳을 기준으로 한다. 그러므로 결정 경계의 관한 식은 $\delta_{1}(x) - \delta_{2}(x)=0$이 된다.
- 여기서 LDA는 공유 공분산을 가지므로 $\Sigma_{1}=\Sigma_{2}=\Sigma$이다. $\Sigma$은 대칭 행렬이므로 $A\cdotp\Sigma\cdotp B == B\cdotp\Sigma\cdotp A$ 이 성립한다. 이를 이용하여 정리하면
- 결정 경계는 $y=Ax+b$의 1차 직선의 방정식 형태가 나오게 되는데 이때 y의 값에 따라 다음 그림과 같이 결정 경계가 움직인다.
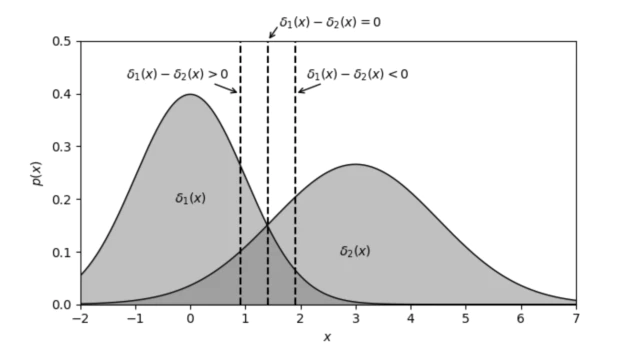
공유 공분산이 아닐 경우($\Sigma_{1} \ne \Sigma_{2}$) 펼치기
- $x^{\top}\mathbf{A}x + \mathbf{B}x + \mathbf{C}$의 형태로 결정 경계는 2차 곡선의 모양으로 그려진다.
고유값(eigen value) 고유 벡터(eigen vector)
-
행렬 A를 선형 변환으로 봤을때, 선형 변환 A에 의해 변환 결과가 자기 자신의 상수배 $\lambda$가 되는 0이 아닌 벡터를 고유 벡터(eigen vector)라고 하고 이때 상수배 $\lambda$를 고유값(eigen value)라고 한다. 이때 고유값은 최대 n개 까지 존재할 수 있음.
-
$n \times n$의 정방행렬 A과 0이 아닌 vector $v$에 대해 다음이 성립.
- A의 고유값과 고유 벡터가 n개 있다고 하면 선형 변환 A를 다음과 같이 표현이 가능하다.
- 관련된 연산들
- 행렬의 Determinant는 라플라스 전개로 계산.
Code Review
[출저][Deep Mahalanobis Detector] Paper github
1. get training sample mean covariance
training sample를 pretrained Model 통과 시킨 Feature들의 mean과 covariance를 계산한다.
class mean 계산
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def sample_estimator(model, num_classes, feature_list, train_loader):
...
for data, target in train_loader:
output, out_features = model.feature_list(data)
# get hidden features
for i in range(num_output):
out_features[i] = out_features[i].view(out_features[i].size(0), out_features[i].size(1), -1)
out_features[i] = torch.mean(out_features[i].data, 2)
# construct the sample matrix
for i in range(data.size(0)):
label = target[i]
if num_sample_per_class[label] == 0:
out_count = 0
for out in out_features:
list_features[out_count][label] = out[i].view(1, -1)
out_count += 1
else:
out_count = 0
for out in out_features:
list_features[out_count][label] \
= torch.cat((list_features[out_count][label], out[i].view(1, -1)), 0)
out_count += 1
num_sample_per_class[label] += 1
sample_class_mean = []
out_count = 0
for num_feature in feature_list:
temp_list = torch.Tensor(num_classes, int(num_feature)).cuda()
for j in range(num_classes):
temp_list[j] = torch.mean(list_features[out_count][j], 0)
sample_class_mean.append(temp_list)
out_count += 1
...

이미지를 사전훈련된 모델에 통과시켜 총 5개층의 hidden layer로 부터 feature를 추출한다. 추출한 feature map ($1\times 64(C) \times 32(H) \times 32(W)$)을 channel 방향으로 평균 ($1 \times 64 $) 을 낸다. 전체 이미지에 대해 feature level와 class 별로 concat 시켜 list_feature를 만든다. list_feature의 크기는 $5 \times 10$ 크기의 list로 3행 4열에는 class 4의 이미지에서 level 3 feature layer에서 뽑힌 feature를 말한다. list_feature 각 level, class 별로 모인 feature들을 class의 수로 평균을 내어 class mean를 만든다. class mean은 channel과 데이터 수로 평균을 낸 최종 feature를 level과 class별로 계산한 것이다.
covariance 계산
covariance는 class mean과 다르게 전체 class가 공유하는 값을 계산한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def sample_estimator(model, num_classes, feature_list, train_loader):
...
precision = []
for k in range(num_output):
X = 0
for i in range(num_classes):
if i == 0:
X = list_features[k][i] - sample_class_mean[k][i]
else:
X = torch.cat((X, list_features[k][i] - sample_class_mean[k][i]), 0)
# find inverse
group_lasso.fit(X.cpu().numpy())
temp_precision = group_lasso.precision_
temp_precision = torch.from_numpy(temp_precision).float().cuda()
precision.append(temp_precision)
...

위 그림처럼 feature vector에 mean vector를 뺀 matrix를 통해 feature에 대한 covariance matrix를 계산한다.
Model-Resnet34과 TrainDataset-CIFAR-10에서 class mean [[10, 64], [10, 64], [10, 128], [10, 256], [10, 512]]과 Covariance Matrix [[64, 64], [64, 64], [128, 128], [256, 256], [512, 512]]가 결과 값으로 계산된다.
2. get Mahalanobis Score of test sample
Training Sample의 mean과 covariance를 통해 Test Sample의 Mahalanobis Score를 계산한다.

Test Sample Batch을 각 layer에 통과시켜 feature map을 추론하고 channel에 대해 평균을 취해 mean feature vector을 계산한다. mean feature vector $x$을 모든 class에 대해 $(x-\mu_c)^\top \Sigma^{-1} (x-\mu_c)$을 계산하여 최대값을 가지는 class의 score만 추출하여 모든 batch에 대해 평균을 취하여 Loss를 구한다. Loss를 backward시켜 Image의 gradient를 구하여 Batch Image에 다음과 같은 노이즈를 추가한다.
\[Noised\;Image = Batch\;Image + magnitude \times Sign(Image.gradient)\]

Noised Image를 다시 위와같이 layer를 통과시키고 같은 연산을 반복하여 Mahalanobis score를 추론한다.
3. Logistic Regression
논문에서는 CIFAR-10의 Test Dataset을 In-distribution으로 사용하고 나머지 SVHN, Tiny ImageNet, LSUN을 Out-distribution으로 사용했다. In, Out-distribution에 대하여 Mahalanobis Score를 구하고 일부 데이터만(CIFAR-10의 10,000개중 1,000개 SVHN 26,032개중 1,000개) 학습에 사용했다. In-distiribution인 CIFAR-10은 Label 0을 부여하고 Out-distribution인 SVHN은 1을 부여했다. 학습에 쓰이지 않은 나머지 데이터로 ROC curve를 그려 AUROC를 측정함.
실제 적용
논문에서는 CIFAR-10의 Train Dataset을 통해 class mean과 covariance를 구하고 구한 다변량 가우시안 확률 분포를 통해 CIFAR-10의 Test Datset과 SVHN의 일부 데이터의 Mahalanobis Score를 구하고 , CIFAR-10 데이터에는 라벨 0을 부여하고 SVHN는 라벨 1을 부여하여 이를 가지고 로지스틱 회귀 함수인 OOD Detector를 통해 나머지 데이터를 추론한다. 이때 실제 상황에서 OOD를 판단할 다변량 가우시안 확률분포의 mean과 covariance를 잘 커버할만큼 많은 Train Dataset을 구하기 힘들다.

Leave a comment