Jean Valjean

In Prison

Lifelong Learning with Dynamically Expandable Networks

[PDF] , Continual Learning, Jaehong Yoon, Eunho Yang, Jeongtae, Sung Ju Hwang

Summary

1. Lifelong learning?

사람은 평생에 걸쳐 외부에서 자극을 받고 이를 통해 무언가를 학습한다. 어떤 행위를 함으로써 고통이 주어진다면 사람은 학습하여 더이상 그 행위를 하지 않는다. 이런 외부 자극이 평생에 걸쳐 끊임 없이 주어지고 이를 계속 학습하지만 사람은 이전의 자극에 대한 학습이 바로 사라지지 않고 기억에 남게 된다.

사람처럼 기계나 프로그램도 끊임 없이 새로운 task가 주어지고 이를 계속 학습하는 방법을 평생 학습(lifelong learning)이라고 한다.

1.1 Lifelnong learning의 특징

  • Multi Task Learning으로 모델이 사람처럼 단일 작업이 아닌 여러 작업에서 범용적으로 사용할 수 있어야함.

  • 학습 데이터가 정체되어있는 offline learning이 아닌 학습 데이터가 실시간으로 들어오는 online learning이 가능해야 됨.

  • 지식 공유(transfer learning)을 통해 새로운 task와 연관성이 높은 정보를 이전 task로 부터 추출 가능해야됨.

    • 사람은 새로운 형태의 자동차를 봐도 이 물체를 자동차라고 인식한다. 이전 데이터에서 자동차의 보편적인 특징을 활용해서 유추함.
1.2 why deep nueral network?

  • 단순히 layer의 weight를 공유하는 매우 직관적인 방법으로 transfer learning이 가능함.

  • 새로운 학습 데이터혹은 새로운 task가 들어올때마다 모델의 weight를 update해줌으로써 continual learning, Multi task learning이 가능함.

하지만 이런 weight 공유라던지 모델을 단순히 재학습하는 방법에서 Catastrophic forgetting, Semantic drift 문제가 발생한다. 새로운 task에 대한 학습이 진행되는 동안 weight가 큰 폭으로 변해 이전 task의 feature 정보들을 망각하거나 feature의 정보가 의미적으로 변하면서 이전 task에 대한 성능이 급격하게 떨어지는 현상을 말한다.

2. 연구 동향

lifelong learning에 해한 연구는 catastrophic forgetting, semantic drift를 방지하고 네트워크를 좀더 효율적으로 사용하거나 학습 속도를 높이는데 초점을 맞추고 있다.

  1. Elastic Weight Consolidation

    Elastic Weight Consolidation(EWC)는 Google Deep Mind에서 나온 논문으로, 데이터셋을 학습하면서 해당 데이터셋에서 중요한 역할을 하는 weight를 찾아 이후 추가 학습에서 이 weight가 변하지 않도록 학습을 진행한다.

    EWC는 다음과 같이 Loss fuction에서 $F_{i}$(Fisher information matrix)를 활용하여 reluarization을 한다. A는 이전 Task를 B는 새로운 TASK를 의마한다.

    \[L(\theta) = L_{B}(\theta) + \sum_{i}{\frac{\lambda}{2} F_{i} ( \theta_{i} - \theta^{*}_{A,i} )^{2}}\]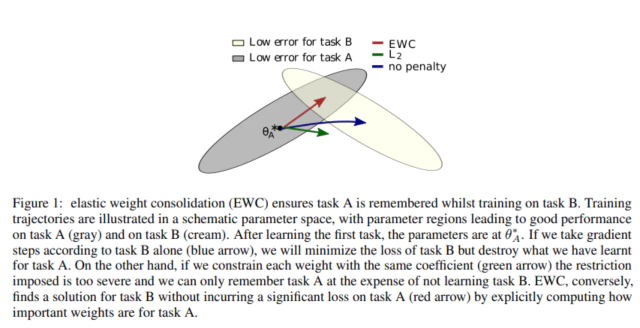

    일반적인 trasfer learning과 EWC의 차이

    회색 범위는 이전 Task A에서 Loss가 낮은 Weight parameter 범위를 나타내고 연노랑색은 새로운 Task B에서 Loss가 낮은 Weight parameter의 범위를 나타낸다.

    Task A에 대해 학습한 현재 parameter의 위치가 $\theta_{A}^{*}$이고 새로운 Task B에 대해 학습을 진행한다고 가정한다.

    파란색 화살표인 Loss function에 어떤 regularization도 없을 경우 weight는 그대로 Task B에 대해 Loss가 가장 적은 중앙 부분으로 학습이 진행된다. 이 경우 Task A에 대한 Loss가 높아지고 성능이 떨어지므로 catastrophic forgetting 현상이 발생한다.

    반면에 초록색 화살표는 이러한 Weight parameter의 변화를 막고자 $l_2$ regularization을 적용했지만 weight의 update(변화)가 적어 Task A와 Task B에 대한 성능이 둘다 좋지 않게 변한다.

    EWC로 학습한 빨간색 화살표는 Weight parameter에서 Task A와 연관도가 높은 부분은 $F_{i}$를 통해 제약을 가해 최대한 변하지 않도록 하고 나머지 부분을 Task B에 대한 학습을 진행하여 두 Task가 겹치는 범위로 최대한 이동한다.

  2. Progressive Network [Rusu et al.(2016)]

    Google Deepmind에서 발표한 논문으로 deep nueral netowrk의 구조를 변형하여 catastrophic forgetting이 일어나는 것을 막은 방법이다.

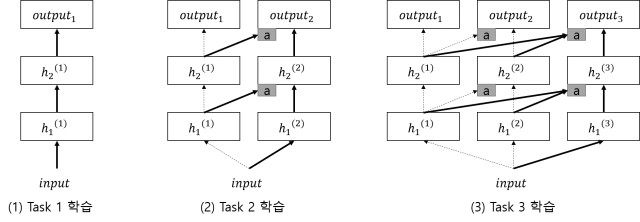
    progressive network 방법

    [그림 출저 - https://realblack0.github.io/2020/03/22/lifelong-learning.html]

    새로운 Task t가 추가될때마다 t-1시점의 network에 sub-network를 추가한다. t-1시점의 network의 weight를 고정시켜 catastrophic forgetting을 방지하고 Task t와 연관도가 높은 weight를 활용하여 sub network를 학습시킨다.

    논문에서 이런 측면 연결(lateral connection)을 통해 knowledge transfer해서 효율적인 학습을 진행한다.

  3. Dynamically Expandable Networks(DEN)

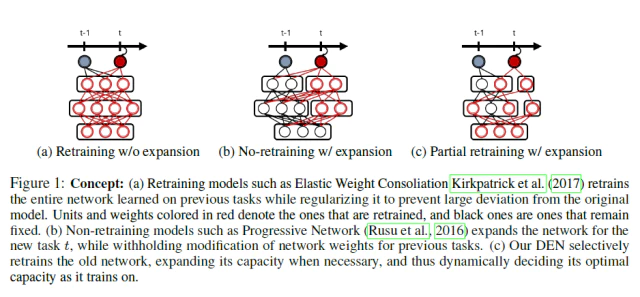
    DEN과 다른 lifelong learning 방법과 비교

    DEN과 다른 lifelong learning 방법인 EWC, progressive network의 차이점을 보여주는데 EWC는 네트워크 확장없이 weight를 선택하여 최대한 변하지않도록 regularizer를 통해 제약하고 progressive network는 고정된 크기의 sub network를 추가하여 학습을 진행한다.

    이와 다르게 DEN은 다음과 같은 효율적인 방법으로 학습을 진행한다.

    • 재학습을 하는 과정에서 EWC와 마찬가지로 새로운 Task와 관련된 Weight만 선택하여 재학습하는 Selective Retraining 과정

    • Progressive Network와 같이 Task가 추가됨에 따라 필요한 만큼의 네트워크의 크기를 늘려 새로운 Task를 수용할 수 있는 Dynamically Network Expansion 과정

    • 재학습 이후 이전과 현재 weight를 비교해서 semantic drift가 발생한 weight를 쪼개서 이전 task에 대한 feature를 유지하는 split/duplication 과정

Method

논문에서 lifelong learning를 연속적인 시간 $t=1,…,t,…,T$에서 시점 t에 들어오는 task $t$의 training dataset인 $D_{t}= \lbrace x_{i}, y_{i} \rbrace^{N_{t}}_{i=1} $를 학습하는 문제로 생각했다.

이때, 각각의 task $t$는 single-task이거나 sub-task로 구성된 multi-task가 될 수도 있다. 시점 $t$에서 이전 시점 $t-1$의 weight parameter만 사용이 가능하고 task $1$ 부터 task $t-1$까지의 dataset은 다시 사용이 불가능하다고 가정했다.

다음의 수식을 통해 학습을 진행하여 task $t$에 대한 model parameter $\bf{W}^{t}$을 얻는 것을 목표로 한다.

\[\underset{\bf{W}^{t}}{minimize} \; \mathcal{L}(\bf{W}^{t}; \bf{W}^{t-1}, \, \mathcal{D}_{t}) + \lambda \, \Omega(\bf{W}^{t}), \; t=1,...,T\]

새로운 task $t$가 들어오면 $t$시점의 dataset $\mathcal{D}_{t}$와 이전 $t-1$시점의 model parameter $\bf{W}^{t-1}$을 이용하여 Loss function $\mathcal{L}$구하고 $t$시점의 model parameter $\bf{W}^{t}$는 regularizer $\Omega$와 $\lambda$를 통해 페널티를 준다.

DEN은 다음과 같이 차례대로 3가지 과정으로 알고리즘이 구성되어 있다. 각각의 과정에서 regularizer는 다르게 적용되고 적용되는 weight 범위도 달라진다.

  1. Selective Learning
  2. Dynamic Network Expansion
  3. Split & Duplication

논문에서 설명한 3가지 과정에 대한 그림

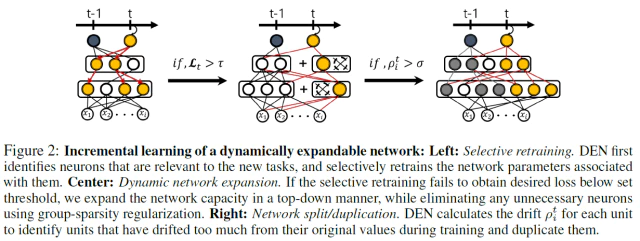
맨 처음 task 1이 도착하면 3가지 알고리즘을 사용하지 않고 다음과 같이 $l_{1}$-regularization으로 sparse한 weight가 나오도록 학습을 진행한다.

\[\underset{\bf{W}^{t=1}}{minimize} \; \mathcal{L}(\bf{W}^{t=1}; \, \mathcal{D}_{t}) + \mu \, \sum^{L}_{l=1}{ \| \bf{W}^{t=1}_{l} \|_{1}}\]

이후 task 2부터 순서대로 다음 알고리즘을 수행한다. 자세한 설명을 위해 Dataset MNIST-Variation을 사용하여 다음과 같은 hidden layer 2개를 가지는 간단한 네트워크에서 각 알고리즘이 수행되는 과정을 그림으로 설명한다.

$y \in \lbrace 0,1 \rbrace$인 binary classification으로 예시를 들었다. 10개의 label중 1개를 postive로 설정하고 나머지 label을 negative로 설정함

1. Selective Learning

build connection & selective learning

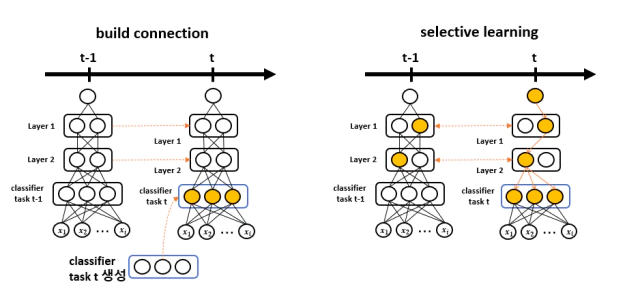
위 그림(왼쪽)처럼 task $t$가 들어오면 task $t$에 대한 classifier를 새로 만들어 task $t-1$의 classifier와 교체하고 이전 classifier는 저장한다. classifier를 제외한 나머지 layer를 고정시키고 다음의 식으로 색칠된 부분인 classifier만 학습한다.

\[\underset{\bf{W}^{t}_{L,t}}{minimize} \, {\mathcal{L}( \bf{W}^{t}_{L,t}; \, \bf{W}^{t-1}_{1:L-1}, \, \mathcal{D}_{t} ) + \mu \| \bf{W}^{t}_{L,t} \|_{1} }\]

여기서 $\bf{W}^{t}_{L,t}$는 $t$시점의 최상단인 L번째 layer의 weight parameter를 뜻한다.

하단의 layer를 고정하고 classifier를 $l_1$-regularizer으로 학습시키면 task $t-1$에서 task $t$와 유사한 feature를 가진 부분은 값이 올라오고 전혀 관련없는 feature는 값이 올라오지 않아 학습과정에서 현재 task에 관련된 부분의 feature를 제외한 나머지가 0인 sparse matrix가 된다.

classifer에서 현재 task와 관련된(0이 아닌) feature weight와 연결되어 있는 하단 layer의 모든 weight들을 따로 떼어내 sub-network $S$를 구성한다. 위 그림(오른쪽)처럼 구성된 sub-network $S$에서만 task $t$의 데이터셋을 다음의 식으로 학습한다.

\[\underset{\bf{W}^{t}_{S}}{minimize} \, \mathcal{L} ( \bf{W}^{t}_{S} ; \, \bf{W}^{t-1}_{S^{\complement}} , \, \mathcal{D}_{t}) + \mu \| \bf{W}^{t}_{S} \|_{2} + \lambda \| \bf{W}^{t-1}_S - \bf{W}^{t}_S \|^{2}_{2}\]

현재 task와 관련된 weight만 선택한 부분 재학습은 coputational overhead를 낮추고 선택되지 않은 부분은 재학습의 영향을 받지 않기 때문에 negative transfer가 일어나지 않아 catastrophic forgetting, semantic drift의 발생 가능성을 낮춘다.

selective learning에서 선택된 Sub network $S$만으로 task $t$를 잘 표현할 수 있다면 학습 과정에서의 Loss가 잘 수렴할 것이다. 하지만 Sub network $S$만으로 표현이 불가능하면 Loss가 잘 수렴하지 않으면 network의 크기(capacity)가 부족하다고 판단하고 다음 단계인 네트워크 확장으로 넘어간다.

2. Dynamic Network Expansion

Network Expansion stage 1

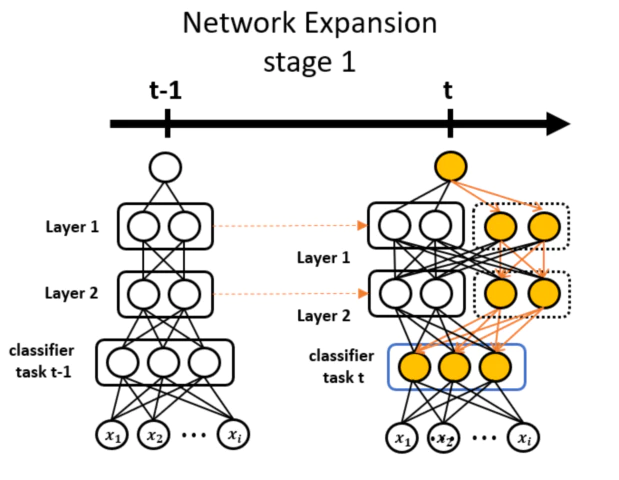
위 그림처럼 고정된 수(k=2)의 weight parameter를 classifier를 제외한 각 layer에 추가한다. 그리고 추가된 weight와 classifier의 weight 부분만 다음식으로 학습을 진행한다. 색이 칠해지지 않은 곳은 단순 값 계산만 하고 weight update 하지 않는다.

\[\underset{\bf{W}^{\mathcal{N}}_{\mathcal{l}}}{minimize} \, \mathcal{L}(\bf{W}^{\mathcal{N}}_{\mathcal{l}} \, ; \bf{W}^{t-1}_{\mathcal{l}} , \, \mathcal{D}_{t}) + \mu \| \bf{W}^{\mathcal{N}}_{\mathcal{l}} \|_1 + \gamma \sum_{\mathcal{g}} { \| \bf{W}^{\mathcal{N}}_{\mathcal{l,g}} \|_{2} }\]

여기서 $\bf{W}^{\mathcal{N}}_{\mathcal{l}}$는 추가된 weight를 말하고 $g \in \mathcal{G}$는 같은 feature를 묶은 weight 그룹이다.

weight가 추가되면서 기존 네트워크에서 잡지 못한 task $t$의 새로운 feature를 학습하게 되어 task $t$에 대한 성능이 향상된다. 그리고 마지막 term에 있는 group sparsity regularization 때문에 학습 도중 불필요한 weight group은 전체적으로 비활성화(0으로 수렴) 된다.

Network Expansion stage 2

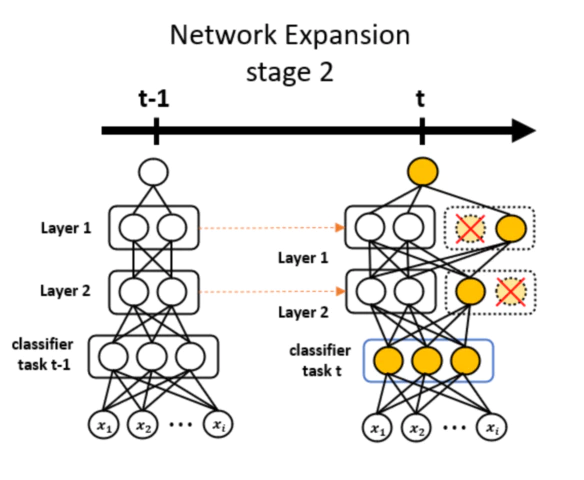
학습과정에서 비활성화된(0으로 수렴) 부분을 그림 처럼 가지치기 해주면 네트워크가 task $t$에 대해 필요한 만큼의 weight를 효율적으로 추가해 줄 수 있다.

3. Split & Duplication

앞선 과정에서 task $t$를 잘 수행하는 network를 만들었다면 이 과정에서는 task $t-1$에서 얻은 feature들을 잊어 버리지 않도록 보존처리하는 과정이다. 각 weight에서 catastrophic forgetting, semantic drift가 발생했는지 아닌지를 검사해서 보존할지 말지를 결정한다.

split & duplication 과정

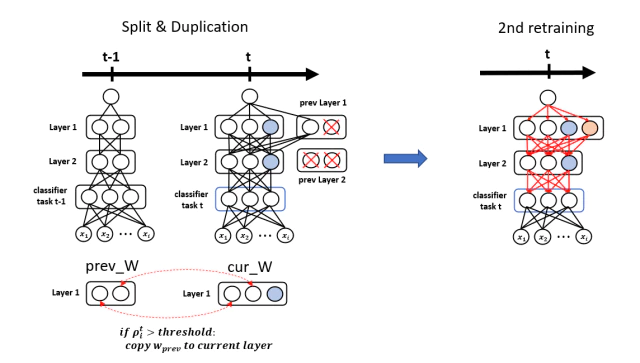
weight에서 semantic drift가 발생했는지 여부는 $\rho^{t}_i = || \bf{w}^{t}_{i} - \bf{w}^{t-1}_{i} || _{2}$을 계산해서 판단한다. 식에서 알 수 있듯이 기존 $t-1$으로 부터 weight 값이 크게 변한 경우 $\rho^{t}_i$값이 크게 계산되고 semantic drift가 발생했다고 간주한다.

prev_W와 cur_W의 weight로 $\rho^{t}_i$을 계산하고 그 값이 threshold 보다 크면 network에 그림처럼 추가되고 작으면 X표처럼 삭제된다.

$\rho^{t}_i$가 큰 weight는 재학습과정에서 의미가 변질되어 task $t-1$의 성능을 하락시킬 가능성이 높다. 이렇게 변질된 weight들은 task $t$ 학습전에 저장된 이전 weight값들을 복사하여 현재 network에 추가해서 이전 task $t-1$의 지식을 보존한다.

network의 구조가 전체적으로 변경되었기 때문에 다시 연결성을 확보하기 위해 다음식으로 재학습을 한다. 이미 대부분의 weight가 optimal하기 때문에 재학습 과정은 빠르게 수렴하게 된다.

\[\underset{\bf{W}^{t}}{minimize} \, \mathcal{L}(\bf{W}^{t} ; \mathcal{D}_{t}) + \lambda \| \bf{W}^{t} - \bf{W}^{t-1} \|^{2}_{2}\]
실제 예시 펼치기/접기

실제 예시

784($28 \times 28$)의 이미지를 입력으로 받고 ReLU를 활성함수로 사용하고 2개의 hidden layer(312-128)를 가지는 network를 사용함.

task 1 - initial

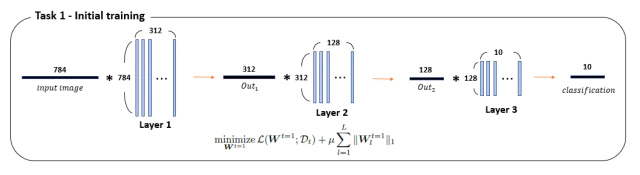
처음 task 1에서 $l_1$-regularization으로 weight를 sparsity하게 만들도록 학습한다.

이후 새로운 task 2가 들어오면 layer 3(task 1)을 저장하고 layer 3(task 2)를 새로 만들어 교체한다. 나머지 layer 1, 2는 고정시켜놓고 layer 3(task 2)만 다음식으로 학습한다.

\[\underset{\bf{W}^{t}_{L,t}}{minimize} \, {\mathcal{L}( \bf{W}^{t}_{L,t}; \, \bf{W}^{t-1}_{1:L-1}, \, \mathcal{D}_{t} ) + \mu \| \bf{W}^{t}_{L,t} \|_{1} }\]

select weight feature

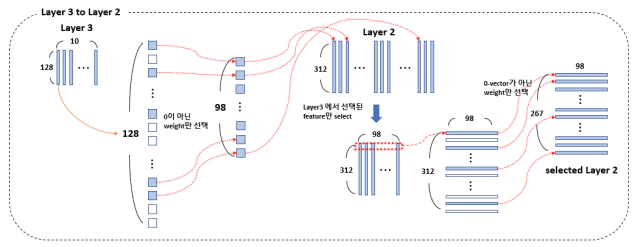
  • 코드상에서 Layer 3에서 0번째 class의 feature만 검사해서 feature selection하는 이유(논문에 설명이 없어서 추측)

같은 task에 대해서 class를 구분짓는 feature는 어차피 모든 class에서 유사하게 사용될 가능성이 높다. class 2나 class 7를 구별하기 위해 사용되는 feature는 유사함. 그렇기 때문에 class 0의 feature weight가 0인지 아닌지만 검사

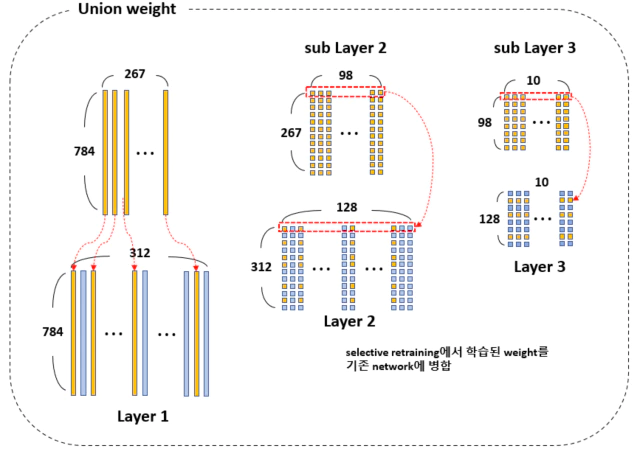
위 그림처럼 현재 task 2와 관련 없는 feature는 앞선 학습 과정에서 0으로 수렴한다. 연관이 높은 부분의 feature(0이 아닌 weight)만 선택하고 같은 index를 가진 feature를 layer 2에서도 선택한다.

layer 3와 연결성을 확보한 layer 2에서 행으로 0-벡터가 아닌 weight를 선택하여 최종 sub layer 2를 얻는다.

select weight feature

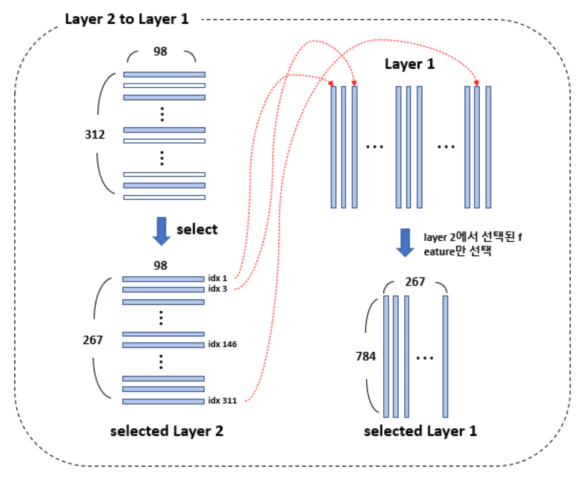
layer 2에서 선택된(행으로 0-벡터가 아닌) index와 똑같은 feature를 layer 1에서 선택해서 sub layer 1을 만든다. 앞서 선택된 sub layer들로 구성된 sub-network $S$를 다음과 같이 학습 시킨다.

select weight feature

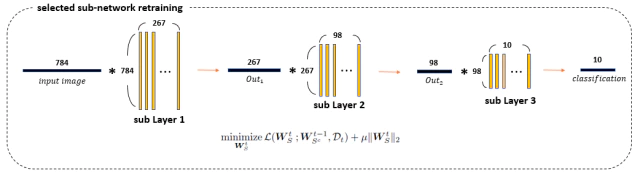
학습이 완료된 sub-network $S$를 원래 network와 다시 합쳐준다.

union weight

selective retraining이후 Loss값이 threshold값보다 높으면 선택된 sub network만으로 새로운 task를 수용할 크기가 부족하다고 판단한다.

network expansion

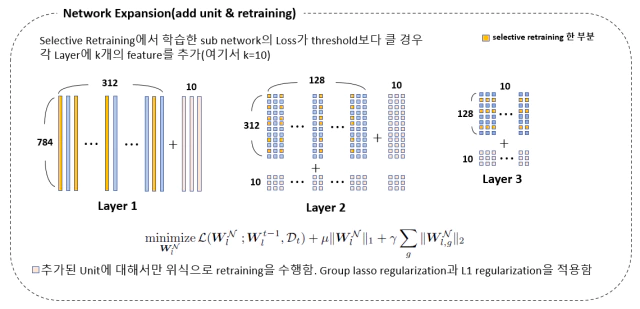
그림처럼 고정된 수(k=10)만큼의 weight를 각 layer에 추가해준다. layer 2 처럼 중간에 있는 layer는 앞선 layer 1의 dim에 맞춰 증가시켜준다. 추가된 weight에 대해서만 group lasso regularization와 $l_1$-regularization을 적용해서 학습한다.

추가된 유닛 제거

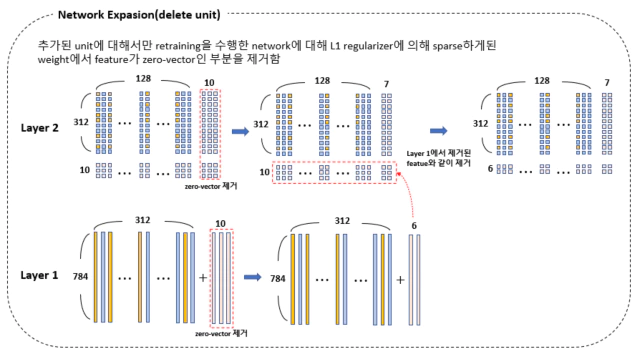
앞서 추가된 weight에 대한 학습이 끝나면 weight에서 sparse한 부분들이 만들어지고 이 부분을 필요없는 weight로 판단하고 삭제한다. 열벡터로 0-벡터이면 삭제하고 유기적으로 연결된 layer의 weight도 삭제해준다. 예를 들어 layer 1에서 10개중 4개가 삭제되고 이에 연결된 layer 2의 하단 부분에서 같은 부분인 4개를 삭제한다.

다음과 같이 catastrophic forgetting을 방지하기 위해 split & duplication 과정을 진행해준다.

split & duplication

위 그림에서 layer 1(task $T-1$)와 layer 1(task $T$)의 weight 벡터를 서로 비교하여 변이된 정도가 많이 크면 layer 1(task $T-1$)의 weight를 layer 1(task $T$)에 추가한다.

split & duplication

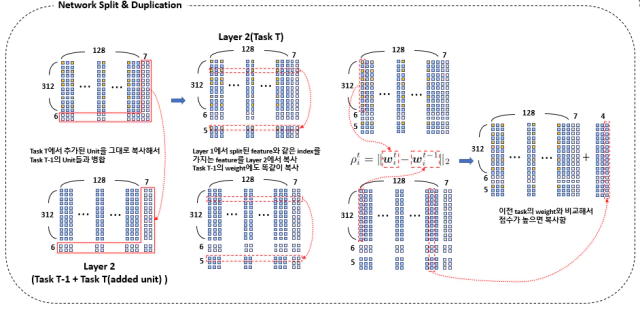
layer 2에서는 layer의 모양을 똑같이 해주기 위해서 layer 2(Task $T$)의 추가된 부분을 layer 2(Task $T-1$)에 그대로 붙여 준다. 앞서 layer 1에서 복사된 index와 같은 위치에 있는 weight들을 복사해서 아래에 추가한다. 이후에 네트워크가 확장되기전의 부분만 서로 비교하고 이때 복사는 추가된 부분까지 해준다.

Reference

https://realblack0.github.io/2020/03/22/lifelong-learning.html

논문 해석

논문 해석 펼치기/접기

[1] Introduction

  • Lifelong Learning (Thrun, 1995)은 연속적으로 task들이 주어지는 continual learning인데 transfer learning에서 매우 중요한 주제이다.

    • lifelong learning의 가장 중요한 목표는 앞서 주어진 task의 지식을 활용하여 더나은 성능을 얻는 것이나 이후의 task들에 대하여 모델이 빠른속도로 수렴하거나 학습되는 것이다.

  • 이 문제를 해결하기 위해 많은 다른 접근법들이 존재하지만, deep neural network의 성능을 최대한 이용하기위해 딥러닝기반의 lifelong learning을 고려함.

  • 딥러닝에서 knowledge를 저장하거나 전달하는 것은 학습된 network weight를 통한 직관적인 방법으로 가능하다.

  • 학습된 weight는 현재 task에 대한 knowledge로서 보조 역할을 할수 있고 new task는 weight를 단순히 공유함으로써 knowledge를 향상시킬수 있다.

  • 그러므로 lifelong learning을 deep neural network의 경우에서 단순히 online 또는 incremental learning의 특수한 경우로 생각할 수 있게 됬다.

  • 이러한 incremental learning(Rusu et al. 2016; Zhou et al. 2012)은 다양한 방법으로 수행된다.

  • 가장 단순한 방법은 새로운 학습 데이터로 network를 계속해서 학습하면서 network를 new task에 대해 점진적으로 fine-tune하는 것이다.

    • 하지만 이런 단순한 네트워크의 재학습은 이전과 신규 task 둘다 성능이 떨어질 수 있다.

  • 만약 동물의 이미지를 분류하는 이전 task와 자동차의 이미지를 분류하는 new task와 같이 2개의 성질이 매우 다르다면 이전 task에서 얻은 knowledge는 new task에서 사용하지 못할 가능성이 높다.

  • 동시에 representation의 원래 의미로부터 멀어져 더이상 old task에 대해 최적화 되있지 않기 때문에 ,new task에 대해 재학습된 representation들은 old task에 대해 부정적인 영향을 미친다.

  • 예를들어, 얼룩말의 얼룩무늬를 표현하는 feature는 이후의 얼룩무늬 티셔츠나 fence와 같은 class들을 분류하는 task에서 이러한 feature에 대해 학습하는 동안 의미가 크게 변할 것이다.

  • 어떻게 deep neural newtork의 online/incremental learning에서 네트워크를 통한 knowledge 공유가 모든 task에서 좋은 성능을 가질수 있는 것 대해 보증할 것인가?

  • 최근 연구는 new task에 대해 good solution을 가지면서 parameter의 값이 크게 변하는 것을 방지하는 regularizer(Kirkpatrick et al. 2017)를 사용하거나 old task의 parameter의 변화를 막는 것(Rusu et al. 2016)을 제안한다.

  • 각 task t마다 new task들은 이전의 학습된 newtwork에서 관련된 부분만 이용하거나 학습시키고 필요에 의해 network의 용량을 확장하기 때문에, 논문에서 제안한 방법은 2개의 접근법과는 다르다.

  • 각각의 task t는 이전 task로 부터 서로 다른 sub-network를 사용하면서 여전히 이전 task와 sub-network의 많은 중요한 부분을 공유 한다.

Figure 01. 다른 lifelong learning method와 비교

  • Figure 1은 현존하는 deep lifelong learning 방법들과의 차이점을 보여준다.

  • dynamic layer expansion과 selecitve parameter sharing을 가진 incremental deep learning setting에서는 해결해야될 많은 과제들이 있다.

    1) 학습과정에서 효율성과 확장성이 좋아야한다. 만약 network의 용량이 증가하면 이후의 task는 더 큰 network의 연결을 만들기 때문에 task 마다 training cost는 점점 증가 할 것이다. 그러므로 retraing의 computaitional overhead를 낮게 유지하는 방법이 필요하다.

    2) network를 확장할 때 얼만큼의 neuron을 추가할지 결정해야한다. 만약 new task를 설명하는데 old nework로 충분하다면 network의 용량을 확장하지 않아도 된다. 다른의미로 현재의 task와 예전 task가 매우 다르면 많은 수의 neuron을 추가할 필요가 있다. 그러므로 모델은 효율성을 위해 오직 필요한 수의 nueron만을 유동적으로 추가할 필요가 있다.

    3) catastrophic forgetting, semantic drift을 방지하는 것. 여기서 catastrophic forgetting, semantic drift는 초기의 학습했던 네트워크의 의미로 부터 멀어지고 그러면서 이전 example과 task에 대한 성능이 하락하는 현상을 말한다. 제안 방법은 나중에 학습된 task에 대해 부분적으로 네트워크를 재학습하고 old subnetwork에 연결되면서 이전 task에 부정적인 영향을 미칠수 있는 새로운 neuron 추가하므로 semantic drift를 방지하는 메커니즘이 필요합니다.

  • 이러한 도전과제들을 극복하기 위해 Dynamic Expandable Networks(DEN)이라고 명명된 효율적이고 성능이 좋은 incremental learning algorithm을 가진 특별한 deep network model을 제안한다.

  • lifelong learning scenario에서 DEN은 필요할때 neuron을 쪼개거나 복사하고 추가하는 방법으로 유동적으로 network의 용량을 증가시키면서 new task에 대한 예측을 효율적으로 학습하기 위해 모든 이전 task에서 학습된 network을 최대한 활용한다.

  • 이 방법은 covoluiton networks를 포함한 일반적인 모든 deep network에 적용이 가능하다.

  • 다양한 공용 dataset에서 lifelong learning에 대해 논문의 incremental deep neural network을 평가했고 각 task에 대해 학습한 분리된 network 모델의 11.9%에서 60.3%의 비율에 해당하는 parameter만을 사용하여 더 높거나 비슷한 성능을 가졌다. 게다가 모든 task에 대해 학습된 network를 fine-tuning하는 것은 심지어 더 나은 성능을 얻었고 배치 모델보다 0.05%에서 4.8%만큼 더 높은 성능을 가졌다. 그러므로 제안모델은 배치 학습이 가능할때 네트워크가 가질수 있는 최대한의 성능을 얻기 위해 네트워크 structure estimation에도 사용될 수 있다.

[2.1] Lifelong learning

  • Lifelong learning(Thrun, 1995)은 이전 task에 얻은 knowledge를 이후 task에 전달하면서 task의 흐름으로 부터 모델을 학습 시키는 continual learning에 대한 learning paradigm(이론적 틀)이다. Thrun(1995)의 아이디어로부터 시작했고 자율 주행과 로봇 학습과 같은 데이터가 연속적인 stream으로 들어오는 상황때문에 이를 연구하는데에는 매우 많은 비용이 들어갔다.

  • Lifelong learning은 떄때로 online-task learning problem으로 해결되기도 하는데 여기서 knowledge transferring만큼 efficient learning에도 초점이 맞춰졌다.

  • Eaton & Rulvolo(2013)는 task의 sequence에서 각 task의 predictor를 학습하기 위해 이전 task에 연관된 부분을 제거함으로써 latent parameter를 효율적으로 업데이트하는 multi-task learning formulation(Kumar & Daume III, 2013)을 기반으로하는 online lifelong learning framework(ELLA)를 제안했다.

  • 최근 lifelong learning은 deep learning framework에서 연구되는데 단순한 re-training으로 deep network의 lifelong learning이 직관적으로 이루어지기 때문이다.

  • 이러한 lifelong learning 연구의 주요한 초점은 catastrophic forgetting을 극복하는 것이다 (Kirkpatrick et al. 2017; Rusu et al., 2016; Zenke et al. 2016; Lee et al. 2017).

[2.2] Preventing catastrophic forgetting

  • deep network의 Incremental learning, lifelong learning은 catastrophic forgetting으로 알려진 문제가 발생한다. catastrophic forgetting은 new task에 대해 학습한 network가 이전 task에서 학습한 것을 forgetting하는 상황을 말한다.

  • 이러한 문제를 해결하기 위해 $l_{2}$-regularizer와 같이 이전에 학습된 것으로 부터 모델이 많이 벗어나지 못하도록 regularizer를 통해 제약을 가하는 것이다.

  • 하지만 단순히 $l_{2}$-regularizer를 사용하는 것은 new task에 대한 new knowledge를 학습하는 것을 막고 이는 차후의 들어오는 task에 대해 sub optimal한 성능을 가지게 된다.

  • 이러한 한계점을 극복하기 위해, Kirkpatrick et al. (2017)은 Elastic Weight Consolidation(EWC)라고 불리는 방법을 제안했다. 이 방법은 이전과 현재 task 모두에 대해 good solution을 찾는 것을 가능하게 하면서 현재 task에 대한 Fisher information matrix를 통해 매 step마다 이전 step의 모델 parameter로 현재 parameter를 조정하는 것이다.

  • Zenke et al. (2017)도 유사한 방법을 제안 했지만 이 방법은 per-synapse consolidation online을 계산하는 방법이고 final parameter 값을 고려하기 보단 전체 learning tranjectory를 고려한다.

  • catastrophic forgetting을 방지하기 위한 또다른 방법은 이전 네트워크에서 변화가 일어나는 것을 완전히 막고 Rusu et al.(2016)에서 한것과 같이 매 learning stage마다 고정된 양의 sub network만큼을 확장하고 원래의 network으로부터 들어오는 weight를 통해 학습하는 것이다.

[2.3] Dynamic network expansion

  • 학습동안에 유동적으로 네트워크의 용량을 증가시키는 neural network에 대한 연구는 매우 적다.

  • Zhou et al. (2012)은 high loss를 가지는 difficult example 그룹에 대한 새로운 뉴런을 추가함으로써 점진적으로 denoising autoencoder를 학습하는 것을 제안했다. 그리고 쓸모없는 중복을 방지하기 위해 다른 뉴런들과 새로운 뉴런을 합치는 작업을 추가했다.

  • 최근에, Philipp & Carbonell(2017)은 nonparametric neural network를 제안했는데 loss를 최소화할 뿐만아니라 각 layer의 차원수를 최소화 한다. 이 때 각 layer는 무한개의 뉴런을 가진다고 가정한다.

  • Cortes et al.(2016)은 boosting 이론에 기반하여 loss를 최소화하는 weight와 structure 모두에 적용되어 학습할수 있는 network를 제안했다.

  • 하지만 이러한 연구중에 multi-task 설정을 고려한 것은 없고 반복적으로 뉴런이 추가되는 과정과 관련된 것은 없다. 반면에 제안 방법은 각 task마다 한번만 network를 학습할뿐만 아니라 매 번 얼만큼의 뉴런이 추가될 것인지를 결정한다.

  • Xiao et al. (2014) multi class classification에 대해 점진적으로 network을 학습시키는 방법을 제안했다. 여기서 network는 용량을 증가시킬뿐만 아니라 모델에 새로운 class가 도착할때 마다 계층 구조를 형성한다.

  • 하지만 이 모델은 top layer에 대해서만 용량이 증가하고 우리의 방법은 전체 레이어에서 뉴런의 수가 증가한다.

[3] Method

  • 연손적인 데이터 흐름에서 모델에 도달하는 학습 데이터의 분포에 대해 알수 없고 몇개의 task가 도달할지도 모르는 lifelong learning scenario에서의 deep neural network의 incremental training 문제로 간주했다.

  • 특히, 우리의 목표는 $t=1,…,t,…,T$에서 $t$시점에 들어오는 training data를 $D_{t}=\lbrace x_{i}, y_{i} \rbrace^{N_{t}}_{i=1}$이라하고 한계가 정해지지않은 $T$개의 task가 연속적으로 들어오는 과정에서 모델을 학습하는 것이다.

  • 각 task $t$는 single task가 될수도 있고 sub task들로 구성된 복합 task일수도 있다.

  • 반면에 논문의 방법은 어떠한 task에 대해서도 포괄적으로 동작하지만 단순화를 위해 input feature $x \in \mathbb{R}^{d}$에 대해 $y \in \lbrace 0, 1 \rbrace$인 binary classification에 대해서만 고려했다.

  • 현재 시점 $t$에서 이전의 모든 $1$부터 $t-1$시점까지의 training dataset을 사용하지 못하는 것이 lifelong learning 설정에서 가장 중요한 도전 과제이다.(오직 이전 task에 대한 모델 parameter만 사용 가능하다.)

  • t시점의 lifelong learning agent는 다음의 수식을 해결함으로써 model parameter $\bf{W}^{t}$를 학습하는 것을 목표로 한다.

\[\underset{\bf{w}^{t}}{maximize} \; \mathcal{L}(\bf{W}^{t}; \bf{W}^{t-1}, \mathcal{D}_{t}) + \lambda \Omega(\bf{W}^{t}), \quad t=1, ...\]

  • 여기서 $\mathcal{L}$은 특정한 task의 loss 함수, $\bf{W}^{t}$는 task $t$에 대한 parameter 그리고 $\Omega(\bf{W}^{t})$는 모델 $\bf{W}^{t}$를 적절하게 강화하는 regularization(element-wise $\mathcal{l}_{2}$ norm)이다.

  • 주로 흥미가 있는 neural network의 case에서 $\bf{W}^{t}=\lbrace \bf{W}_{l} \rbrace^{L}_{l=1}$은 weight tensor를 나타내고 $l$은 Layer의 level을 뜻한다.

  • lifelong learning의 이러한 도전 과제들을 해결하기 위해, network가 이전 task로 부터 얻은 knowledge를 최대한 활용하도록 하고 현재까지의 축적된 knowledge만으로 new task를 설명하기에 충분하지 않을 때 네트워크의 크기를 유동적으로 확장 할수 있도록 했다.

  • Figure 2와 Algorithm 1에서 이러한 incremental learning process를 설명했다.

Algorithm 1 Incremental Learning of a Dynamically Expandable Network

Input: Dataset $\mathcal{D}=(\mathcal{D_{1}}, …, \mathcal{D}_{T})$, Thresholds $\tau,\sigma$
Output: $\;\bf{W}^{T}$

for $\; t=1,…,T\;$ do
$\quad$if $\;t=1\;$ then
$\quad\quad$Train the network weights $\bf{W}^{1}$ using Eq.2
$\quad$else
$\quad\quad \bf{W}^{t}=\it{SelectiveRetraining}(\bf{W}^{t-1})$ {using Algorithm 2}
$\quad\quad$if $\;\mathcal{L}_{t}>\tau$ then
$\quad\quad\quad \bf{W}^{t}=\it{DynamicExpansion}(\bf{W}^{t})$ {using Algorithm 3}
$\quad\quad \bf{W}^{t}=\it{Split}(\bf{W}^{t})$ {using Algorithm 4}

  • 다음의 subsection에서 incremental leraning algorithm의 자세한 사항인 1)Secltvie retraining 2)Dynamic network expansion 3)Network split/duplication 에 대해서 설명한다.
[3.1] Selective Retraining

  • 연속적인 task 흐름에서 모델을 학습시키는 가장 무식한 방법은 new task가 도착할때 마다 전체 모델을 재학습하는 것이다.

    • 하지만 이러한 재학습과정은 deep neural network에서는 매우 계산 비용이 많이 든다.

    • 그러므로 net task에 의해 영향을 받는 weight에 대해서만 재학습하는 모델의 selective retraining 과정을 제안한다.

  • 초기(t=1)에, network를 $\mathcal{l}_{1}$-regularization으로 weight를 sparsity(희소)하게 만들고 이러한 결과로 각 뉴런이 다음층의 layer와 매우 적은 수의 뉴런만 연결된다.

\[\underset{\bf{W}^{t=1}}{minimize} \; \mathcal{L}(\bf{W}^{t=1}; \, \mathcal{D}_{t}) + \mu \sum^{L}_{t=1}{\| \bf{W}^{t=1}_{t} \|_{1}}\]

  • 여기서 $1 \le l \le L$은 netowrk의 $l_{th}$번째 layer를 말하고 $\bf{W}^{t}_{l}$은 layer $l$의 $t$시점의 weight parameter이다. $\mu$는 weight $\bf{W}$에서 sparsity의 정도를 결정하는 $l_{1}$ norm의 regularization paramter이다.

    • convolution layer에서는 filter에 (2,1)-norm를 적용해 이전 layer로부터 매우 적은 수의 filter들만 선택한다.

  • incremental learning 과정 내내 $\bf{W}^{t-1}$은 sparse하게 유지되고 new task와 관련된 sub-network에만 집중하기만 하면 coputational overhead를 급격하게 감소시킬 수 있다.

  • new task $t$가 모델에 도달할 때 다음의 공식을 통해 neural network의 최상단 hidden unit을 사용하여 task $t$를 예측하기 위한 sparse linear model을 학습시킨다.

\[\underset{\bf{W}^{t}_{L,t}}{minimize} \; \mathcal{L}(\bf{W}^{t}_{L,t} ; \bf{W}^{t-1}_{1:L-1}, \, \mathcal{D}_{t}) + \mu \| \bf{W}^{t}_{L,t} \|_{1}\]

  • 여기서 $\bf{W}^{t-1}_{1:L-1}$은 최상단 레이어의 weight $\bf{W}^{t}_{L,t}$를 제외한 모든 다른 weight parameter를 말한다. 즉, layer $L-1$의 hidden unit과 output unit $\omicron_{t}$ 사이의 연결성(connection)을 얻기 위해 위의 optimization을 풀어야한다. (이때, 최상단 layer를 제외한 모든 다른 layer $L-1$까지의 $\bf{W}^{t-1}$는 학습이 되지 않도록 고정한다.)

  • 일단 이 layer에서 sparse connection이 구성되면 학습에의해 영향을 받는 network의 모든 weight와 unit들을 구별할수 있게되고 반면에 $\omicron_{t}$과 연결되지않은 network의 나머지부분은 변하지 않게 된다.

  • 특히 $\omicron_{t}$까지의 경로에 있는 모든 unit을 구별하기 위해 선택된 node로부터 시작하여 network에서 넓이우선탐색(bfs)을 수행한다.

  • 다음의 optimization으로 선택된 Sub-network $S$의 weight $\bf{W}^{t}_{S}$만을 학습한다.

\[\underset{\bf{W}^{t}_{S}}{minimize} \; \mathcal{L}(\bf{W}^{t}_{S}; \, \bf{W}^{t-1}_{S^{\complement}}, \, \mathcal{D}_{t}) + \mu \| \bf{W}^{t}_{S} \|_{2}\]

  • hidden unit 사이에서 이미 sparse connection이 구성되었기 때문에 element-wise $l_{2}$ regularizer만 사용한다.

  • 이러한 부분 재학습은 computational overhead를 낮추고 또한 선택되지 않은 neuron들은 재학습 과정에서 전혀 영향을 받지 않기 떄문에 negative transfer(이전 task의 성능을 하락시키는 학습)를 방지하는데 도움을 준다. Algorithm 2에 이러한 재학습 과정이 설명되어 있다.

Algorithm 2 Selective Retraining

Input : Dataset $\mathcal{D}_{t}$, Previous parameter $\bf{W}^{t-1}$
Output : network parameter $\bf{W}^{t}$

Initialize $l \leftarrow L-1, \; S=\lbrace \omicron_{t} \rbrace$
Solve Eq. 3 to obtain $\bf{W}^{t}_{L,t}$
Add neuron $i$ to $S$ if the weight between $i$ and $\omicron_{t}$ in $\bf{W}^{t}_{L,t}$ is not zero.
for $l=L-1,…,1$ do
$\quad$ Add neuron $i$ to $S$ if there is exists some neuron $j \in S$ such that $\bf{W}^{t-1}_{l,ij} \neq 0.$
Solve Eq. 4 to obtain $\bf{W}^{t}_{S}$

[3.2] Dynamic Network Expansion

  • new task가 이전 task들과 연관성이 높은 경우거나, 이전의 task들로 부터 얻은 축적된 부분지식들이 new task를 설명하기에 충분하다면 new task에서는 selective retraining만 해도 충분할 것이다.

  • 하지만 학습된 feature가 new task를 정확하게 표현하지 못할때, network에 new task를 위해 필수적인 feature(object의 특징)를 설명하기 위한 추가적인 뉴런을 붙일 필요가 있다.

  • Zhou et al. 2012, Rusu et al. 2016와 같은 몇몇 연구도 비슷한 아이디어를 기반으로 한다. 하지만 중복되는 forward pass가지는 학습과정을 반복적으로 수행하기 떄문에 효율적이지 못하고 task의 어려움 정도와 상관없이 각 task t마다 고정된 수의 유닛을 추가하므로 network 크기 효율과 성능면에서 suboptimal하다.

  • 이러한 한계점을 극복하기 위해, 각각의 유닛에서 network의 중복되는 재학습없이 각 task마다 layer에 얼만큼의 neuron을 추가할 것인지 유동적으로 결정하기 위한 효율적인 방법인 group sparse regularization을 사용한다.

  • network의 $l_{th}$ layer는 k개의 고정된 수의 유닛만큼 확장되고 다음의 2개의 parameter matrices expansion을 유도된다. $\bf{W}^{t}_{l}= [ \bf{W}^{t-1}_{l} ; \bf{W}^{\mathcal{N}}_{l}]$과 $\bf{W}^{t}_{l-1}= [ \bf{W}^{t-1}_{l-1} ; \bf{W}^{\mathcal{N}_{l-1}} ]$ 이고 여기서 $\bf{W}^{\mathcal{N}}$은 추가 neuron이 속한 확장된 weight matrix이다.

  • 여기서 항상 모든 k개의 유닛을 추가하고 싶지 않기때문에 다음과 같은 optimization으로 추가된 parameter에 대해 group sparsity regularization을 수행한다.

\[\underset{\bf{W}^{\mathcal{N}_{l}}}{minimize} \; \mathcal{L}( \bf{W}^{\mathcal{N}}_{l}; \, \bf{W}^{t-1}_{l}, \, \mathcal{N}_{t} ) + \mu \| \bf{W}^{\mathcal{N}}_{l} \|_{1} + \gamma \sum_{g}{ \| \bf{W}^{\mathcal{N}}_{l,g} \|_{2} }\]

  • 여기서 $g \in \mathcal{G}$는 각 뉴런에 대해 들어오는 weight들을 묶은 그룹이다. convolutional layer에서는 각 conv filter에 대응되는 activation map을 각 그룹으로 지정했다.

  • 이 group sparsity regularization은 full network에서 적절한 수의 neuron을 찾기 위해 사용된 논문들이Wen et al.(2016), Alvarez & Salzmann(2016) 있다. 하지만 본 논문에서는 이를 부분적인 network에 적용했다. Algorithm 3에서 expansion 과정에 대해 설명한다.

  • selective retraining이 끝나고 network는 적당한 threshold 밑으로 Loss가 떨어졌는지를 체크한다. 만약 Loss가 떨어지지 않았다면 k개의 neuron만큼 각 layer를 확장하고 Eq.5의 optimization을 진행한다.

  • Eq.5에 있는 group sparsity regularization 때문에 학습에서 불필요하다고 여겨지는 hidden unit(혹은 convolutional filters)는 전체적으로 비활성화될 것이다.

  • 이런 dynamic network expansion process로부터 모델이 $\bf{W}^{t-1}_{l}$에 의해 표현되지 못하는 새로운 feature를 잡아낼 수 있다고 기대되어지고 반면에 많은 유닛이 추가되는 것을 방지하면서 network의 크기를 효율적으로 사용할 수 있게 된다.

Algorithm 3 Dynamic Network Expansion

Input : Dataset $\mathcal{D}_{t}$, Threshold $\tau$

Perform Algorithm 2 and compute $\mathcal{L}$
if $\mathcal{L} \ge \tau$ then
$\quad$ Add $k$ units $\mathcal{h}^{\mathcal{N}}$ at all layers
$\quad$ Solve for Eq. 5 at all layers
for $l=L-1, …, …1$ do
$\quad$ Remove useless units in $\mathcal{h}^{\mathcal{N}_{l}}$

[3.3] Network Split/Duplication

  • lifelong learning에서 가장 중요한 도전 과제는 semantic drift와 catastrophic forgetting 문제이다. 모델이 나중에 들어온 task에 대해 점진적으로 학습하면서 이전 task에서 학습된 것들을 잊고 전체적인 task에 대한 성능이 떨어지는 것을 말한다.

  • semantic drift를 막는 가장 간단하지만 대중적인 방법은 원래의 parameter의 값으로 부터 크게 벗어나지 않도록 $l_{2}$-regularization을 사용하여 다음과 같이 제약하는 것이다.

\[\underset{\bf{W}^{t}}{minimize} \; \mathcal{L}(\bf{W}^{6}; \, \mathcal{D}_{t}) + \lambda \| \bf{W}^{t} - \bf{W}^{t-1} \|^{2}_{2}\]

  • 여기서 $t$는 현재 task를 의미하고 $\bf{W}^{t-1}$는 task $\lbrace 1, …, t-1\rbrace$ 에서 학습된 network의 weight tensor를 의미한다. $\lambda$는 regularization parameter이다.

  • 이 $l_{2}$ regularization은 optimization에서 $\bf{W}^{t}$가 $\bf{W}^{t-1}$와 근접하는 solution을 찾도록 강제한다. 주어진 $\lambda$의 크기에 따라 $\lambda$가 작으면 이전 Weight와의 차이가 커도 되므로 이전 task에 대해서 잊는 반면 새로운 task에서 많이 학습할 것이다. 반면에 $\lambda$가 크면 이전 weight와의 차이가 커지면 안되므로 이전 task에 대해서 가능한한 보존 하려고 노력하면서 학습할 것이다.

  • 단순히 $l_{2}$ regularization을 사용하기 보단 Fisher information(Kirkpaatrick el al.2017)으로 각 element에 가중치를 주는 것이 가능하다.

  • 그럼에도 불구하고, task의 수가 커지거나 이후의 들어오는 task들이 의미적으로 이전 task와 많이 동떨어져 있으면 새로운 task와 이전 task에 대해서 모두 좋은 성능을 가지는 solution을 찾기 힘들어진다.

  • 이러한 상황에서 더 나은 solution은 서로 다른 2개의 task에 대해 optimal한 feature를 가지는 neuron을 분리하는 것이다.

  • Eq.6 optimization 이후 시점 t-1와 t의 weight들 사이의 $l_{2}$-distance을 계산하여 각 hidden unit $i$에 대해서 semantic drift된 정도 $\rho^{t}_{i}$를 측정한다.

  • 만약 $\rho^{t}_{i} > \sigma$ 이면 학습 과정에서 feature의 의미가 급격하게 변화한 것으로 간주하고 이 neuron $i$를 2개의 복사본으로 쪼갠다(복제에 적절한 새로운 edge를 추가한다).

    • 이러한 split/duplication 과정은 동시에 모든 hidden unit에서 진행될 수 있다.

  • neuron의 복제 이후 split은 전체적인 network 구조를 변화시키기 때문에 network는 optimization Eq.6에 의해 다시 weight를 학습할 필요가 있다.

  • 하지만 실제로 이러한 2번째 재학습은 이미 첫번쨰 학습에서 대부분의 parameter들이 optimal한 위치에 있기 때문에 대부분 빠른 속도로 수렴하게 된다.

  • Algorithm 4에 이러한 split 과정에 대해 설명되어 있다.

Algorithm 4 Network Split/Duplication

Input: Weight $\bf{W}^{t-1}$, Threshold $\sigma$

Perform Eq.6 to obtain $\overline{\bf{W}}^{t}$
for all hidden unit $i$ do
$\quad \rho^{t}_{i}=| w^{t}_{i} - w^{t-1}_{i} |_{2}$
$\quad$if $\rho^{t}_{i} > \sigma$ then
$\quad\quad$Copy $i$ into $i’$ ($w’$ introduction of edges for $i’$)
Perform Eq.6 with the initialization of $\overline{\bf{W}}^{t}$ to obtain $\bf{W}^{t}$

[3.4] Timestamped Inference

  • network expansion과 network split 모든 과정에서 각각의 새롭게 추가된 unit $j$에 대해 $\lbrace z \rbrace_{j}=t$와 같이 network에 추가된 시점이 t 학습 시점이라고 기록된다. 게다가 이러한 timestamping은 새로운 hidden unit이 추가되면서 생기는 sementic drift를 방지할 수 있다.

  • inference time 각 task는 stage t에서 추가된 parameter만을 사용하고 학습 과정에서 추가된 new hidden unit으로 old task를 inference하는 것을 방지한다.

  • 이런 전략은 split되지 않고 학습된 unit들을 통해 이후의 task에서 학습한 것으로부터 이익을 얻기 떄문에 Rusu et al.(2016)에서 각 학습 stage마다 weight를 고정하는 것보다 더 유연하다.

[4] Experiment

[4.1] Experiment Setting
[4.1.1] Baselines and out model

1) DNN-STL : Base Deep Neural Network이고 feedforward, convolutional 각 task는 독립적으로 학습함

2) DNN-MTL : Base DNN으로 모든 task를 한꺼번에 학습함

3) DNN-L2 : Base DNN으로 각 task t에서 $\bf{W}^{t}$는 $\bf{W}^{t-1}$으로 초기화되고 $\bf{W}^{t-1}$와 $\bf{W}^{t}$사이의 $l_{2}$-regularization으로 연속적으로 학슴함

4) DNN-EWC : regularization을 위한 Elastic Weight Consolidation(Kirkpatrick et al.2017)으로 DNN Network를 학습함

5) DNN-Progressive : Rusu et al.2016의 Progressive network를 구현하고 이후 task가 도달하면 network weight를 고정되도록 유지한다.

6) DEN : Dynamically Expandable Network

[4.1.2] Base network settings

1) FeedForward networks : ReLU를 활성함수로 사용하고 312-128개의 neuron을 가지는 2개의 layer network를 사용했다.

2) Convolutional networks : 실험은 CIFAR-100 dataset에서 진행하고 AlexNet(Krizhevsky et al.2012)의 수정된 버전을 사용했다. $5 \times 5$ filter size를 가지는 5개의 convolution layers(64-128-256-256-128 detpth)와 3개의 FC Layer (384-192-100 neuron)를 사용함.

[4.1.3] Datasets

1) MNIST-Variation : 62,000개의 0부터 9까지의 손글씨 이미지로 구성되어있고 MNIST와 다르게 예측을 어렵게 하기 위해 손글씨에 임의의 각도로 회전되거나 배경에 노이즈를 가지고 있다. 각각의 class에 대한 6,200개의 이미지를 1,000/200/5,000개의 이미지를 train/val/test 으로 쪼개서 사용했다. 각 task에서 한개의 class만 positive로 정의하고 나머지는 negative로 정의한 one-versus-rest binary classification으로 설정했다.

2) CIFAR-100 : 100개의 포괄적인 object class의 60,000장의 이미지로 구성되었다. 각 class는 학습을 위한 500장의 이미지와 test를 위한 100장의 이미지를 갖고 있다. 이 데이터셋으로 실험하기 위해 base network로 CNN을 사용하고 CNN에 제안방법이 적용가능하다는 것을 보여줌. 게다가 각 task는 10개의 subtask로 구성했고 각각의 class에서 binary classification을 진행했다.

3) AWA(Animals with Attributes) : 50종의 동물 class를 가지는 30,475개의 이미지로 구성된 데이터셋이다(Lampert et al. 2009). PCA로 차원수가 500까지 줄어든 데이터셋에서 제공하는 DECAF feature를 사용했다. 이미지를 랜덤으로 30/30/30개로 쪼개 train/valid/test로 사용함.

[4.2] Quantitative Evaluation

figure 3

figure 3

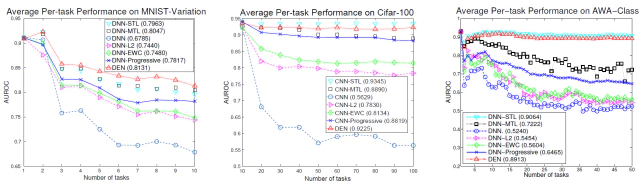
  • 제안 모델을 효율성과 예측 정확도라는 관점에서 평가했고 효율성은 학습 시간과 학습이 끝나는 시점에서의 network 크기로 측정했다.

  • Figure 3의 처음 행에 제안 모델과 baseline의 average per-task에 대한 성능 비교를 나타내었다.

  • 각 task에서 최적으로 학습되기 때문에 DNN-STL은 CIFAR-100과 AWA dataset에서 가장 좋은 성능을 보인다. 반면에 다른 모든 모델들은 semantic drift가 발생할 수 있는 실시간 학습(online learning)이기 때문에 성능이 낮다.

  • task 수가 적을 때는 다중 과제 학습을 통한 지식 공유에서 MTL이 가장 잘 작동하지만 task 수가 많을 때는 MTL보다 학습 능력이 크기 때문에 STL이 더 잘 작동한다.

  • DEN은 이러한 batch model와 거의 비슷하거나 MNIST-Variation dataset에서는 성능이 더 앞선다.

  • L2와 EWC와 같이 regularization과 결합된 재학습 모델은 비록 전자보다 후자가 성능이 더 뛰어나지만 전체적으로 좋지 않은 성능을 가진다.

    • L2, EWC은 유동적으로 네트워크의 크기를 조절하지 못하는 모델이기 때문에 성능 약화가 일어날 수 밖에 없다.

  • Progressive network는 앞선 2개의 모델보다는 성능이 좋지만 모든 데이터의 경우에서 DEN보다 성능이 좋지 않았다.

  • task의 수가 가장 크고 적절한 네트워크 크기를 찾는데 어려운 AWA dataset에서의 성능폭 차이가 가장 중요하다.

  • 만약 네트워크가 너무 작으면 new task를 표현하기 위한 학습 능력을 충분히 갖출 수 없고 반대로 네트워크 크기가 너무 크면 overfitting하기 쉽다.

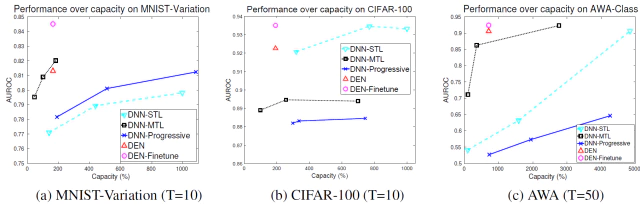
  • 각 dataset에서 MTL과 비교하여 측정된 network capacity에 대한 각 모델의 성능을 실험했다.

  • baseline과 비교하여 다른 network capacity를 가지는 여러개의 모델에 대한 성능을 실험했다. DEN은 Progressive network보다 상당히 적은 수의 parameter로 더 나은 성능을 가지고 이와 반대로 같은 수의 parameter를 사용할 경우 더 좋은 성능을 얻었다.

  • DEN은 오직 STL의 18.0%, 60.3%, 11.9%의 네트워크 크기만을 가지고 MNIST-Variation, CIFAR-100, AWA에서 같은 수준의 성능을 얻었다. 이러한점은 DEN의 유동적으로 network의 최적 크기를 찾아준다는 가장 중요한 이점을 보여준다. MNIST-Variation에서는 매우 작은 모델로 학습되고 반면에 CIFAR-100에서는 상당히 큰 network로 학습된다.

  • 게다가 모든 task에 대한 DEN 모델의 fine-tuning은 모든 dataset에서 가장 좋은 성능을 보여준다. 이는 DEN이 lifelong learning 뿐만아니라 모든 task를 이용가능할 떄 network 크기를 추정하는데에도 사용할 수 있음을 보여준다.

[4.2.1] Effect of selective retraining

figure 4 (a), (b)

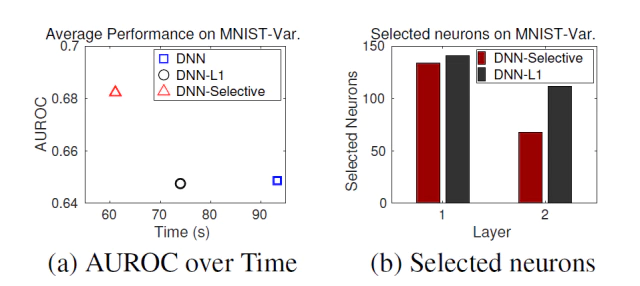
  • MNIST-Variation dataset에서 Area Under ROC(AUROC)와 학습 속도를 측정하여 selective retraining이 얼마나 효율적이고 효과적인지를 실험했다.

  • DNN-selective(network 확장이 없는 버전)라고 불리는 모델과 대응하여 DNN-L2와 DNN-L1에서 재학습된 모델을 정확도와 효율성면에서 비교한다.

  • Figure 4(a)는 GPU computation의 실제 시간으로 측정된 학습 시간과 정확도를 보여준다. 각 모델을 살펴 보면 selective retraining이 full retraining보다 매우 적은 학습 시간을 가지고 심지어 sparse network weight를 가지는 DNN-L1 보다도 더 적다.

  • 게다가 DNN-L1은 DNN-L2보다 낮은 정확도를 가지는 반면 DNN-Selective는 base network보다 2% 향상된 정확도를 가진다.
    • 이러한 성능 향상은 DEN이 각각의 새롭게 추가된 task에 대해 일부분의 subnetwork만 학습시켜서 catastrophic forgetting이 발생하는 것을 방지했기 때문이다.

  • Figure 4(b)은 selective retraining중인 각 layer에서 선택된 neuron의 수를 보여준다.

  • DNN-Selective은 task-specific한 상단 부분의 Layer에서는 상당히 적은 유닛이 선택되고 반면에 포괄적인 부분을 담당하는 저레벨의 layer 유닛은 많은 부분이 선택된다.
    • low level layer는 주로 낮은 수준의 feature 예를들어 edge, color, corner와 같은 대부분의 물체에서 발견할 수 있는 포괄적인 부분을 잡는 경우가 많고 반면에 high level layer 높은 수준의 feature 얼굴, 바퀴와 같이 낮은 수준의 feature들이 합쳐진 물체의 형상을 잡는 경우가 많음. 그래서 high level layer은 task에 따라가 크게 변하는 경우가 많고 low level layer은 어떤 task가 오든 공통적인 부분이 많음. DNN-Selective에서 상단 부분의 layer는 task에 따라 달라지므로 new task와 연관된 neuron이 적어 선택된 수가 적고 하단 부분의 layer는 모든 물체에서 발견할수 있는 저수준의 feature가 많아 new task와도 연관된 neuron이 많아서 선택된 수가 많다.
[4.2.2] Effect of network expansion

figure 4 (c)

  • network expansion의 효과를 selective retraining과 layer expansion을 한 제안 모델의 다양한 변종들을 비교했고 network split은 진행하지 않았다. 이런 모델들을 실험에서 DNN-Dynamic라고 명명함.

  • DNN-Dynamic를 메인 실험에서 사용된 DNN-L2와 비교하고 DNN-Constant와도 비교했다. DNN-Constant는 MNIST-Variation dataset에서 고정된 수의 unit을 각 layer에 추가하여 제안 모델을 확장시키는 버전이다.

  • Figure 4(c)는 이러한 실험 결과를 보여주는데, DNN-Dynamic AUROC에서 가장 좋은 성능을 얻었고 DNN-Constant를 포함한 모든 모델보다 성능이 높았다. 하지만 DNN-Dynamic의 network 증가된 크기는 DNN-Constant(k=20)보다 매우 작았다.

  • 이렇게 적은 수의 parameter는 갖는 점은 학습 효율면에서도 이점을 가질뿐만 아니라 모델의 overfitting을 방지하는데도 강점을 갖는다.

  • DNN-Constant의 network 크기를 DEN과 유사한 수준인 k=13으로 설정해서 좋은 성능을 얻었지만, 여전히 각 layer에 대해 유동적으로 neuron의 수를 적용하는 DEN의 성능보다는 좋지 않았다.

[4.2.3] Effect of network split/duplication and timestamped inference

figure 5

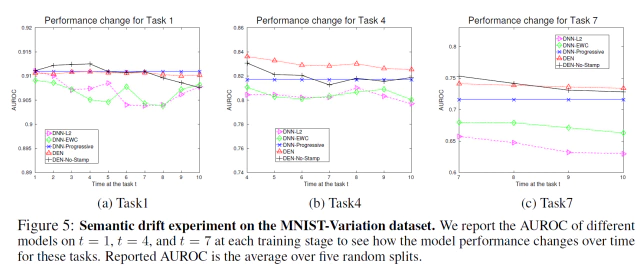
  • network split/duplication과 unit timestamping이 semantic drift(또는 catastrophic forgetting)를 얼마나 방지하는지를 보여주기 위해 later task에 대해 좋은 성능을 얻으면서, 제안 모델의 성능을 basline과 DEN-No-Stamp(timestamping이 없는 버전)과 같은 DEN의 변종과 비교했다.

  • Figure 5에서 (a), (b), (c)는 각각 training stage t가 t=1, t=4, t=7일때의 모델의 성능의 성능으 변화를 보여준다.

  • DNN-L2은 앞선 stage에서 모델의 semantic drift를 방지하지만 later task(t=4, 7)에서 점점 성능이 나빠지는 결과를 보여준다.

  • DNN-EWC는 Kirkpatrick et al(2017)에서 실험한 것과 마찬가지로 DNN-L2보다 더나은 성능을 보였다.

  • 하지만 DNN-EWC는 network의 크기 확장을 할수 없기 때문에 제한된 표현 능력을 갖게되어 제안 모델과 DNN-Progressive비해 매우 낮은 성능을 가진다.

  • DNN-Progressive는 모델에서 parameter를 재학습하지 않기 때문에 old-task에서는 sematic drift가 일어나지 않는다.

  • DEN w/o Timestamping은 later task에 대해 DNN-Progressive 보다 더나은 성능을 보이고 task가 진행될수록 생기는 성능저하 폭이 적다.

  • 마지막으로 timestamp inference를 가지는 제안 모델 DEN은 어떤 learning stage에서도 급격한 성능 저하를 볼수 없고 DNN-Progressive보다 성능이 매우 뛰어나다.

  • 이런 실험결과로 DEN이 semantic drift를 방지하는것에는 매우 효과적임을 알 수 있다.

[5] Conclusion

  • lifelong learning에 대한 특별한 DNN인 Dynamically Expandable Network를 제안했다. DEN은 task와의 연관도를 이용하여 old task에 대해 학습한 network의 일부분만 재학습하고 반면에 new task를 설명하기 위한 new knowledge가 필요할때 네트워크가 필요한 최적의 크기를 찾아 크기를 확장했다. 그러면서 모델에서 semantic drift가 발생하는 것을 방지했다.

  • DEN의 convolutional network와 feedforward 둘다에대해 구현했고 lifelong learning scenario에서 다양한 데이터셋을 실험에 사용했다. 현재의 다른 lifelong learning method와 비교하여 매우 큰 성능 향상을 보였고, 성능이 비슷할 경우 약 11.9% - 60.3%의 네트워크 크기만을 사용하여 효율적임을 보였다. 게다가 DEN이 network structure estimation에서도 매우 유용하게 사용될 수 있음을 보여준다.

Leave a comment

Recent posts